Modified Newtonian Dynamics – Is there something to it?

You are constantly accelerating. The Earth’s gravity is pulling you downward at g = 9.8 meters per second per second. It wants to take your velocity up to about 10 meters per second after only the first second of free fall. Normally you don’t fall, because the floor is solid due to electromagnetic forces and also it is electromagnetic forces that give your body structural integrity and power your muscles, resisting the pull of gravity.

You are also accelerating due to the Earth’s spin and its revolution about the Sun.

International Space Station, image credit: NASA

Our understanding of gravity comes primarily from these large accelerations, such as the Earth’s pull on ourselves and on satellites, the revolution of the Moon about the Earth, and the planetary orbits about the Sun. We also are able to measure the solar system’s velocity of revolution about the galactic center, but with much lower resolution, since the timescale is of order 1/4 billion years for a single revolution with an orbital radius of about 25,000 light-years!

It becomes more difficult to determine if Newtonian dynamics and general relativity still hold for very low accelerations, or at very large distance scales such as the Sun’s orbit about the galactic center and beyond.

Modified Newtonian Dynamics (MOND) was first proposed by Mordehai Milgrom in the early 1980s as an alternative explanation for flat galaxy rotation curves, which are normally attributed to dark matter. At that time the best evidence for dark matter came from spiral galaxy rotation curves, although the need for dark matter (or some deviation from Newton’s laws) was originally seen by Fritz Zwicky in the 1930s while studying clusters of galaxies.

NGC 3521. Image Credit: ESA/Hubble & NASA and S. Smartt (Queen’s University Belfast); Acknowledgement: Robert Gendler 

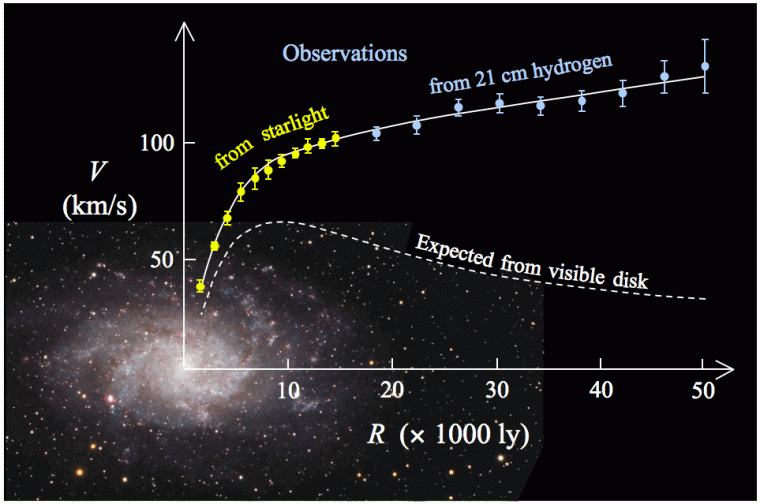
Galaxy Rotation Curve for M33. Public Domain, By Stefania.deluca – Own work,  https://commons.wikimedia.org/w/index.php?curid=34962949

If general relativity is always correct, and Newton’s laws of gravity are correct for non-relativistic, weak gravity conditions, then one expects the orbital velocities of stars in the outer reaches of galaxies to drop in concert with the fall in light from stars and/or radio emission from interstellar gas, reflecting decreasing baryonic matter density. (Baryonic matter is ordinary matter, dominated by protons and neutrons). As seen in the image above for M33, the orbital velocity does not drop, it continues to rise well past the visible edge of the galaxy.

To first order, assuming a roughly spherical distribution of matter, the square of the velocity at a given distance from the center is proportional to the mass interior to that distance divided by the distance (signifying the gravitational potential), thus

   v² ~ G M / r

where G is the gravitational constant, and M is the galactic mass within a spherical volume of radius r. This potential corresponds to the familiar 1/r² dependence of the force of gravity according to Newton’s laws.  In other words, at the outer edge of a galaxy the velocity of stars should fall as the square root of the increasing distance, for Newtonian dynamics.

Instead, for the vast majority of galaxies studied, it doesn’t – it flattens out, or falls off very slowly with increasing distance, or even continues to rise, as for M33 above. The behavior is roughly as if gravity followed an inverse distance law for the force (1/r) in the outer regions, rather than an inverse square law with distance (1/r²).

So either there is more matter at large distances from galactic centers than expected from the light distribution, or the gravitational law is modified somehow such that gravity is stronger than expected. If there is more matter, it gives off little or no light, and is called unseen, or dark, matter.

It must be emphasized that MOND is completely empirical and phenomenological. It is curve fitted to the existing rotational curves, rather successfully, but not based on a theoretical construct for gravity. It has a free parameter for weak acceleration, and for very small accelerations, gravity is stronger than expected. It turns out that this free parameter, , is of the same order as the ‘Hubble acceleration’ . (The Hubble distance is c / H and is 14 billion light-years; H has units of inverse time and the age of the universe is 1/H to within a few percent).

The Hubble acceleration is approximately .7 nanometers / sec / sec or 2 centimeters / sec / year  (a nanometer is a billionth of a meter, sec = second).

Milgrom’s fit to rotation curves found a best fit at .12 nanometers/sec/sec, or about 1/6 of . This is very small as compared to the Earth’s gravity, for example. It’s the ratio between 80 years and one second, or about 2.5 billion. So you can imagine how such a variation could have escaped detection for a long time, and would require measurements at the extragalactic scale.

The TeVeS – tensor, vector, scalar theory is a theoretical construct that modifies gravity from general relativity. General relativity is a tensor theory that reduces to Newtonian dynamics for weak gravity. TeVeS has more free parameters than general relativity, but can be constructed in a way that will reproduce galaxy rotation curves and MOND-like behavior.

But MOND, and by implication, TeVeS, have a problem. They work well, surprisingly well, at the galactic scale, but come up short for galaxy clusters and for the very largest extragalactic scales as reflected in the spatial density perturbations of the cosmic microwave background radiation. So MOND as formulated doesn’t actually fully eliminate the requirement for dark matter.

Horseshoe shaped Einstein Ring

Image credit: ESA/Hubble and NASA

Any alternative to general relativity also must explain gravitational lensing, for which there are a large number of examples. Typically a background galaxy image is distorted and magnified as its light passes through a galaxy cluster, due to the large gravity of the cluster. MOND proponents do claim to reproduce gravitational lensing in a suitable manner.

Our conclusion about MOND is that it raises interesting questions about gravity at large scales and very low accelerations, but it does not eliminate the requirement for dark matter. It is also very ad hoc. TeVeS gravity is less ad hoc, but still fails to reproduce the observations at the scale of galaxy clusters and above.

Nevertheless the rotational curves of spirals and irregulars are correlated with the visible mass only, which is somewhat strange if there really is dark matter dominating the dynamics. Dark matter models for galaxies depend on dark matter being distributed more broadly than ordinary, baryonic, matter.

In the third article of this series we will take a look at Erik Verlinde’s emergent gravity concept, which can reproduce the Tully-Fisher relation and galaxy rotation curves. It also differs from MOND both in terms of being a theory, although incomplete, rather than empiricism, and apparently in being able to more successfully address the dark matter issues at the scale of galaxy clusters.

References

Wikipedia MOND entry: https://en.wikipedia.org/wiki/Modified_Newtonian_dynamics

M. Milgrom 2013, “Testing the MOND Paradigm of Modified Dynamics with Galaxy-Galaxy Gravitational Lensing” https://arxiv.org/abs/1305.3516

R. Reyes et al. 2010, “Confirmation of general relativity on large scales from weak lensing and galaxy velocities” https://arxiv.org/abs/1003.2185

“In rotating galaxies, distribution of normal matter precisely determines gravitational acceleration” https://www.sciencedaily.com/releases/2016/09/160921085052.htm