Tag Archives: Dark matter

September 26, 2023

Dark Stars in the Early Universe

By darkmatterdarkenergy
Image Credit: Bill Saxton, ALMA (ESO/NAOJ/NRAO), NRAO/AUI/NSF In this image, from the Atacama Large Millimeter Array in Chile, we are seeing three stars forming from a dusty disk within our own Milky Way. The two objects in the center are separated by 61 astronomical units (Earth-Sun distance is one AU, astronomical unit). One sees evidence of the disk fragmenting to form additional protostars.

Dark Stars is the name given to hypothetical stars in the early universe that were overwhelmingly composed of ordinary matter (baryons [protons and neutrons] and electrons) but that also were ‘salted’ with a little bit of dark matter.

And stars in this category have not evolved to the point of achieving stellar nucleosynthesis in their cores, instead they are, again hypothetically, heated by the dark matter within.

Professor Katherine Freese of the University of Texas physics department (previously at U. Michigan) and others have been suggesting the possibility of dark stars for well over a decade, see “The Effect of Dark Matter on the First Stars: A New Phase of Stellar Evolution”.

In a paper from last year “Dark stars powered by self-interacting dark matter” authors Wu, Baum, Freese, Visinelli, and Yu propose a type of self-interacting dark matter (SIDM). The authors start with the consideration of overdense regions known as ‘halos’ at the epoch of 200 million years for the universe’s age, corresponding to redshift z ~ 20. These are expected due to gravitational instability of slightly overdense regions that we see in the cosmic microwave background maps, from an epoch of only 0.38 million years.

One starts out with these dark matter dominated halos, but the ordinary matter within is much more efficient at collapse since it can radiate energy away electromagnetically. Dark matter, by definition, does not interact electromagnetically, that is why we don’t see it except through its  gravitational effects or if it were to decay into normal matter. That also minimizes its ability to cool and collapse, other than through decay processes.

As the normal matter radiates, cools, and collapses further it concentrates into the center, away from the dark matter halo overall, but would include some modest amount of dark matter. A dark star might be fueled by only 0.1% dark vs. ordinary matter.

New Particles χ, φ

This SIDM scenario requires two new particles that the authors refer to as χ and φ. The χ dark matter particle (a fermion) could have a mass of order 100 GeV, similar to that of the Higgs particle (but that is a boson, not a fermion), and some 100 times that of a proton or neutron.

The φ particle (a scalar field) is a low-mass mediator in the dark sector with a mass closer to that of an electron or muon (heavy electron), in the range of 1 to 100 MeV. This particle would mediate between the χ and ordinary matter, baryons and electrons.

The main mechanism for heating is the decay of the charged χ and its anti-particle into pairs of (neutral) φ particles that can then go on to decay to electron / positron pairs. These easily thermalize within the ionized hydrogen and helium gas cloud as the electrons and positrons annihilate to gamma rays when they meet their corresponding anti-particle.

The decay mean free path for the φ would need to be of order 1 AU or less (an astronomical unit, the Earth-Sun distance); in this way, the decays would deposit heat into the protostellar cloud. The clouds can heat up to thousands of degrees Kelvin such that they are very efficient radiators. And since they can be large, larger than 1 AU their luminosity can also be very large.

A Model Dark Star

In their paper, Wu and co-authors model a 10 solar mass dark star with a photosphere of 3.2 AU radius. Such a dark star if placed at the Sun’s location would have its photosphere beyond the orbits of Earth and Mars and reaching to the outer edge of the asteroid belt. 

The temperature of their model star is 4300 Kelvin, or 3/4 that of the Sun. Despite the lower temperature, because of the large size, the total luminosity in this case is 150,000 times that of our Sun. It would be reddish in color at the source, but highly redshifted into the infrared light would reach us. This luminosity is 100 times more luminous than the most luminous red supergiant star, but not much brighter intrinsically than the (much hotter) blue supergiant Rigel.

Because such a star would be a first stellar generation, it would have no spectral lines from any elements other than hydrogen or helium. Only hydrogen and helium and a trace amount of lithium are formed in the Big Bang.

Black holes as a result?

Other dark stars might have temperatures of 10,000 Kelvin, and possibly accrete matter from the aforementioned halo until they reach luminosities as large as 10 million times that of the Sun. These might be visible with the James Webb Space Telescope (JWST).

Dark stars might last as long as half a billion years, or the annihilation might shut down sooner due to the collapse of ordinary matter in the protostellar envelope. Once the dark star phase ends, there could be a rapid collapse to high mass nucleosynthesis-powered stars that would end their short lives as black holes, or one could even have direct collapse to black holes of high masses. These would be interesting candidates as the seeds of the supermassive black holes of millions and billions of solar masses that we observe today in the centers of galaxies, both nearby and at high redshifts. 

The James Webb Space Telescope is finding more early galaxies than expected within the first 500 million years of the universe. It is able to peer back that far because of its instruments’ sensitivity in the infrared portion of the spectrum. The light from such early galaxies is heavily shifted from optical to infrared frequencies, by order a factor of 10, due to the universe’s expansion over the past 13 billion plus years. Perhaps seeing more early-onset galaxies is in part because of the role that dark stars play in hastening the evolution of the stellar population.

We look forward to JWST detecting the earliest stars, that might be dark stars, or providing constraints on their visibility or viability.

– Stephen Perrenod, Ph.D., September 2023

1 Comment   |  tags: , , , , | posted in Uncategorized

March 10, 2020

Hexaquark Dark Matter: Bosons, but not WIMPy at all

By darkmatterdarkenergy

Dibaryons

Imagine you smash a proton and neutron together. What do you get? Typically you get a deuteron which is the nucleus of deuterium, heavy hydrogen. Deuterium has one electron in its neutral atomic state. And it has two baryons, the proton and neutron, so it is known as a dibaryon.

Now as you have heard, protons and neutrons are really quark triplets, held together by gluons in bound configurations. A proton has two up quarks (electric charge +2/3) and a down quark (charge -1/3) for a net charge of +1 and a neutron has two down quarks and an up quark for a net charge of 0.

These are the two lightest quarks and protons and neutrons are by far the dominant components in the ordinary matter in the universe, mostly as hydrogen and helium.

Quarks, protons, and neutrons are all fermions, particles with half-integer spins (1/2, 3/2, -1/2, etc.).

The other main class of particles is called bosons, and that class includes photons, gluons, the W and Z of the weak interaction, and the never directly observed graviton. They all have integer spins (typically 1, but 0 for the Higgs boson, and 2 for the graviton).

752px-Standard_Model_of_Elementary_Particles.svg

Figure 1: The Standard Model major particles: quarks (purple), leptons (green), force carrier bosons (orange), Higgs boson (yellow) with mass, charge, spin indicated.

Six quarks in a Bag

Suppose you collided a proton and neutron together, each with three quarks, and you ended up with a single six quark particle that was stable. It would be a more exotic type of dibaryon. It would have three up quarks, three down quarks, and it would not be a fermion. It would be a boson, with integer spin, spin 0 or 1, in this case. It would be six quarks in a bag, a bound state held together by gluons.

sixquarksinabag

Figure 2. Six quarks in a bag, a hexaquark

Hexaquark2380

Figure 3. The d* resonance at 2.38 GeV, observed at the Cooler Synchrotron in Julich, Germany

Such a particle has been discovered in the past decade, and is named the d* hexaquark. It is seen as the resonance in Figure 3 above, found in proton-neutron collisions, and has a mass of 2.38 GeV (for reference the proton mass is 0.935 GeV and the neutron mass is 0.938 GeV). It decays to a deuteron and two pions, either neutral as shown in the figure, or charged pions.

It is also possible to produce a d* by irradiating a deuteron with a gamma ray.

The d* was already predicted by the famed mathematician and physicist Freeman Dyson in 1964, working with his collaborator Xuong. Their mass estimate was quite close at 2.35 GeV, using a simple quark model.

Dyson just passed away recently; you may have heard of his Dyson sphere concept. The idea is that an advanced civilization would build a sphere of solid material surrounding its star in order to hold an extremely large population and absorb virtually all of the star’s energy. Larry Niven modified this to a ring in his 1970 sci-fi novel Ringworld.

Hexaquark dark matter

Azizi, Ageav, and Sundu have recently suggested a hexaquark of the form uuddss, that is, two up, two down, and two strange quarks. Their mass estimate is around 1.2 GeV, half that of the d* composed of only up and down quarks. It is expected to be stable with long lifetime.

And also recently, Bashkanov and Watts at the University of York have made a nice proposal that d* could be the dark matter particle. The d* particle is itself unstable, but they propose that stable condensates with many d* particles could form. Their paper,  “A New Possibility for Light-Quark Dark Matter” is here:

https://iopscience.iop.org/article/10.1088/1361-6471/ab67e8/pdf

The d* has one great advantage over the other proposed particles, it has actually been discovered! The d* has a good sized mass for a dark matter candidate, at about 2.5 times the mass of the proton.

The authors find that the d* could form lengthy chains or spherical condensates with thousands to millions of d* particles. Unlike individual d* particles, the condensates could be stable ‘super atoms’ lasting for billions of years.

However to make this work the binding energy would have to exceed the difference between the 2.38 GeV d* mass and the deuteron mass of 2.014mGeV, thus would have to be greater than about 0.4 GeV.

The d* would be produced thermally when the universe was at temperatures in the range from 1 to 3 trillion Kelvins. The condensates would need to form quickly before individual d* particles of short lifetimes decayed away.

The favored candidates for dark matter have been WIMPs, supersymmetric particles. But no supersymmetric particle has ever been detected at the Large Hadron Collider or elsewhere, which is incredibly disappointing for many particle physicists. The other main candidates have been the axion and sterile neutrino, both quite low in mass. These have never been directly detected either; they remain hypothetical.

The d* particle is a boson, and the authors’ theoretical approach is that in the early universe as it cooled, both baryons and dibaryonic matter froze out. The baryons ended up, after the cosmic nucleosynthesis phase as protons, deuterium dibaryons, and helium nuclei (alpha particles, that are composed essentially of two deuterons), the main constituents of ordinary matter.

What would happen to d* under the early conditions of the Big Bang? Bosons like to clump together, into something called Bose-Einstein condensates. Yes, that Einstein. And that Boson. Bose-Einstein statistics were developed in the 1920s and govern the statistics of bosons (integer spin particles), and differ from that of fermions.

To confirm this model would require astronomical observations or cosmic ray observations. Decays of d* particles could result in gamma ray production with energies up to 0.5 GeV. Their decay products might also be seen as upward moving cosmic rays, in Earth-bound cosmic ray experiments. These would be seen coming up through the Earth, unlike normal cosmic rays that cannot penetrate so much ordinary matter, and the decay events would result in gamma rays, nucleons and deuterons, as well as pions as the decay products.

 

Additional reference: http://www.sci-news.com/physics/dark-matter-particle-d-star-hexaquark-08188.html

4 Comments   |  tags: , , , , , | posted in Big Bang & Inflation, Dark Matter, Early Universe

November 11, 2019

Dark Catastrophe, a few Trillion Years away?

By darkmatterdarkenergy

The Equation of State for Dark Energy

The canonical cosmological model, known as ΛCDM, has all matter including CDM (cold dark matter), at approximately 30% of critical density. And it has dark energy, denoted by Λ, at 70%. While the cosmological constant form of dark energy, first included in the equations of general relativity by Einstein himself, has a positive energy, its pressure is negative.

The negative pressure associated with dark energy, not the positive dark energy density itself, is what causes the universe’s expansion to accelerate.

The form of dark energy introduced by Einstein does not vary as the universe expands, and the pressure, although of opposite sign, is directly proportional to the dark energy density. The two are related by the formula

P = – ρ c²

where P is the pressure and ρ the energy density, while c is the speed of light.

More generally one can relate the pressure to the energy density as an equation of state with the parameter w:

P = – w ρ c²

And in the cosmological constant form, w = -1 and is unvarying over the billions of years of cosmological time.

Does Dark Energy vary over long timescales?

String theory (also known as membrane theory) indicates that dark energy should evolve over time.

The present day dark energy may be the same field that was originally much much stronger and drove a very brief period of inflation, before decaying to the current low value of about 6 GeV (proton rest masses) per cubic meter.

There are searches for variation in the equation of state parameter w; they are currently inconclusive.

How much variance could there be?

In string theory, the dark energy potential gradient with respect to the field strength yields a parameter c of order unity. For differing values of c, the equation of state parameter w varies with the age of the universe, more so as c is larger.

When we talk about cosmological timescales, it is convenient to speak in terms of the cosmological redshift, where z = 0 is the present and z > 0 is looking back with a larger z indicating a larger lookback time. If the parameter c were zero then the value of w would be -1 at all redshifts (z = 0 is the current epoch and z = 1 is when the universe only about 6 billion years old, almost 8 billion years ago).

WvsC

This Figure 3 from an article referenced below by Cumrun Vafa of Harvard shows the expected variance with redshift z for the equation of state parameter w. The observationally allowed region is shaded gray. The colored lines represent different values of the parameter c from string theory (not the speed of light). APS/Alan Stonebraker

Observational evidence constraining w is gathered from the cosmic microwave background, from supernovae of Type Ia, and from the large scale galaxy distribution. That evidence from all three methods in combination restricts one to the lower part of the diagram, shaded gray, thus w could be -1 or somewhat less. There are four colored curves, labelled by their value of the string theory parameter c, and it appears that c > 0.65 could be ruled out by observations.

Hubble Constant tension: String theory explaining?

It’s not the constant tension of the Hubble constant. Rather it is the tension, or disagreement between the cosmic microwave background observational value of the Hubble constant, at around 67 kilometers/sec/Megaparsec and the value from supernovae observations, which yield 73 kilometers/sec. And the respective error bars on each measurement are small enough that the difference may be real.

The cosmic microwave background observations imply a universe about a billion years older, and also better fit with the ages of the oldest stars.

It turns out a varying dark energy with redshift as described above could help to explain much of the discrepancy although perhaps not all of it.

Better observations of the early universe’s imprint on the large scale distribution of galaxies from ground-based optical telescope surveys and from the Euclid satellite’s high redshift gravitational lensing and spectroscopic redshift measurements in the next decade will help determine whether dark energy is constant or not. This could help to disprove string theory or enhance the likelihood that string theory has explanatory power in physics.

Tests of string theory have been very elusive since we cannot reach the extremely high energies required with our Earth-based particle accelerators. Cosmological tests may be our best hope, small effects from string theory might be detectable as they build up over large distances.

And this could help us to understand if the “swampland conjecture” of string theory is likely, predicting an end to the universe within the next few trillion years as the dark energy field tunnels to an even lower energy state or all matter converts into a “tower of light states” meaning much less massive particles than the protons and neutrons of which we are composed.

Reference

“Cosmic Predictions from the String Swampland”, Cumrun Vafa, 2019. Physics 12, 115, physics.aps.org

1 Comment   |  tags: , , , , | posted in Dark Energy

April 3, 2019

Modified Gravity

By darkmatterdarkenergy

We don’t Need no Stinkin’ Dark Matter

Extra Acceleration

You’ve heard of dark matter, right? Some sort of exotic particle that lurks in the outskirts of galaxies.

Maybe you know the story of elusive dark matter. The first apparent home for dark matter was in clusters of galaxies, as Fritz Zwicky postulated for the Coma Cluster in the 1930s, due to the excessive galaxy random motions that he measured.

There have been eight decades of discovery and measurement of the gravitational anomalies that dark matter is said to cause, and eight decades of notable failure to directly find any very faint ordinary matter, black holes, or exotic particle matter in sufficient quantities to explain the magnitude of the observed anomalies.

If dark matter is actually real and composed of particles or primordial black holes then there is five times as much mass per unit volume on average in that form as there is in the form of ordinary matter. Ordinary matter is principally in the form of protons and neutrons, primarily as hydrogen and helium atoms and ions. 

Why do we call it dark? It gives off no light. Ordinary matter gives off light, it radiates. What else gives off no light? A gravitational field stronger than predicted by existing laws.

Gravitational anomalies are seen in the outer regions of galaxies by examining galaxy rotation curves, which flatten out unexpectedly with distance from the galactic center.  They are seen in galaxy groups and clusters from measuring galaxy velocity dispersions, from X-ray observations of intracluster gas, and from gravitational lensing measurements. A dark matter component is also deduced at the cosmic scale from the power spectrum of the cosmic microwave background spatial variations.

The excessive velocities due to extra acceleration are either caused by dark matter or by some departure of gravity over and above the predictions of general relativity. 

Actually at high accelerations general relativity is the required model but at low accelerations Newtonian dynamics is an accurate approximation. The discrepancies arise only at very low accelerations. These excess velocities, X-ray emission, and lensing are observed only at very low accelerations, so we are basically talking about an alternative of extra gravity which is over and above the 1/r² law for Newtonian dynamics.

Alternatives to General Relativity and Newtonian Dynamics

There are multiple proposed laws for modifying gravity at very low accelerations. To match observations the effect should start to kick in for accelerations less than c * H, where H is the Hubble expansion parameter and its inverse is nearly equal to the present age of the universe. 

That is only around 1 part in 14 million expressed in units of centimeters per second per second. This is not something typically measurable in Earth-bound laboratories; scientists have trouble pinning down the value of the gravitational constant G to within 1 part in 10,000. 

This is a rather profound coincidence, suggesting that there is something fundamental at play in the nature of gravity itself, not necessarily a rather arbitrary creation of exotic dark matter particle in the very early universe. It suggests instead that there is an additional component of gravity tied in some way to the age and state of our universe.

Do you think of general relativity as the last word on gravity? From an Occam’s razor point of view it is actually simpler to think about modifying the laws of gravity in very low acceleration environments, than to postulate an exotic never-seen-in-the-lab dark matter particle. And we already know that general relativity is incomplete, since it is not a quantum theory.

The emergent gravity concept neatly solves the quantum issue by saying gravity is not fundamental in the way that electromagnetism and the nuclear forces are. Rather it is described as an emergent property of a system due to quantum entanglement of fields and particles. In this view, the fabric of space also arises from this entanglement. Gravity is a statistical property of the system, the entropy (in thermodynamic terms) of entanglement at each point.

Dark Energy

Now we have a necessary aside on dark energy. Do you know that dark energy is on firmer standing now than dark matter? And do you know that dark energy is just described by additional energy and pressure components in the stress-energy tensor, fully described within general relativity?

We know that dark energy dominates over dark matter in the canonical cosmological model (Lambda-Cold Dark Matter) for the universe. The canonical model has about 2/3 dark energy and the solution for the universe’s expansion approximates a de Sitter model in general relativity with an exponential ‘runaway’ expansion.

Dark Gravity

As we discuss this no dark matter alternative, we refer to it as dark gravity, or dark acceleration. Regardless of the nature of dark matter and dark gravity, the combination of ordinary gravity and dark gravity is still insufficient to halt the expansion of the universe. In this view, the dark gravity is due to ordinary matter, there is just more of it (gravity) than we expect, again only for the very low c * H or lower acceleration environments.

Some of the proposed laws for modified gravity are:

  1. MOND – Modified Newtonian Dynamics, from Milgrom
  2. Emergent gravity, from Verlinde
  3. Metric skew tensor gravity (MSTG), from Moffat (and also the more recent variant scalar-tensor-vector gravity (STVG), sometimes called MOG (Modified gravity)

Think of the dark gravity as an additional term in the equations, beyond the gravity we are familiar with. Each of the models adds an additional term to Newtonian gravity, that only becomes significant for accelerations less than c*H. The details vary between the proposed alternatives. All do a good job of matching galaxy rotation curves for spiral galaxies and the Tully-Fisher relation that can be used for analyzing elliptical galaxies.

Things are trickier in clusters of galaxies, which are observed for galaxy velocity dispersions, X-ray emission of intracluster gas, and gravitational lensing. The MOND model appears to come up short by a factor of about two in explaining the total dark gravity implied.

Emergent gravity and modified gravity theories including MSTG claim to be able to match the observations in clusters.

Clusters of Galaxies

Most galaxies are found in groups and clusters.

Clusters and groups form from the collapse of overdense regions of hydrogen and helium gas in the early universe. Collapsing under its own gravity, such a region will heat up via frictional processes and cooler sub-regions will collapse further to form galaxies within the cluster.

Rich clusters have hundreds, even thousands of galaxies, and their gravitational potential is so high that the gas is heated to millions of degrees via friction and shock waves and gives off X-rays. The X-ray emission from clusters has been actively studied since the 1970s, via satellite experiments.

What is found is that most matter is in the form of intracluster gas, not galaxies. Some of this is left over primordial gas that never formed galaxies and some is gas that was once in a galaxy but expelled via energetic processes, especially supernovae.

Observations indicate that around 90% of (ordinary) matter is in the form of intracluster gas, and only around 10% within the galaxies in the form of stars or interstellar gas and dust. Thus modeling the mass profile of a cluster is best done by looking at how the X-ray emission falls off as one moves away from the center of a cluster.

In their 2005 paper, Brownstein and Moffat compiled X-ray emission profiles and fit gas mass profiles with radius and temperature profiles for 106 galaxy clusters. They aggregated data from a sample of 106 clusters and find that an MSTG model can reproduce the X-ray emission with a mass profile that does not require dark matter.

The figure below shows the average profile of cumulative mass interior to a given radius. The mass is in units of solar masses and runs into the hundreds of trillions. The average radius extends to over 1000 Kiloparsecs or over 1 Megaparsec (a parsec is 3.26 light-years).

The bottom line is that emergent gravity and MSTG both claim to have explanatory power without any dark matter for observations of galaxy rotation curves, gravitation lensing in clusters (Brower et al. 2016), and cluster mass profiles deduced from the X-ray emission from hot gas.

galaxyclustermasseswodm.fig2

Figure 2 from J.R. Brownstein⋆ and J.W. Moffat (2005), “Galaxy Cluster Masses without Non-Baryonic Dark Matter”. Shown is cumulative mass required as a function of radius. The red curve is the average of X-ray observations from a sample of 106 clusters. The black curve is the authors’ model assuming MSTG, a good match. The cyan curve is the MOND model, the blue curve is a Newtonian model, and both require dark matter. The point is that the authors can match observations with much less matter and there is no need to postulate additional exotic dark matter.

What we would very much like to see is a better explanation of the cosmic microwave background density perturbation spectrum for the cosmic scale, for either of these dark gravity models. The STVG variant of MSTG claims to address those observations as well, without the need for dark matter.

In future posts we may look at that issue and also the so called ‘silver bullet’ that dark matter proponents often promote, the Bullet Cluster, that consists of two galaxy clusters colliding and a claimed separation of dark matter and gas.

References

Brower, M. et al. 2016, “First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing Measurements” https://arxiv.org/abs/1612.03034v2

Brownstein, J. and Moffat, J. 2005, “Galaxy Cluster Masses without Non-baryonic Dark Matter”, https://arxiv.org/abs/astro-ph/0507222

Perrenod, S. 1977 “The Evolution of Cluster X-ray Sources” http://adsabs.harvard.edu/abs/1978ApJ…226..566P, thesis.

https://darkmatterdarkenergy.com/2018/09/19/matter-and-energy-tell-spacetime-how-to-be-dark-gravity/

https://darkmatterdarkenergy.com/2016/12/30/emergent-gravity-verlindes-proposal/

https://darkmatterdarkenergy.com/2016/12/09/modified-newtonian-dynamics-is-there-something-to-it/

3 Comments   |  tags: , , , , , , , , , | posted in Dark Matter, Gravity

January 27, 2019

Mini Black Holes as Dark Matter?

By darkmatterdarkenergy

Ancient Voyager Satellite Says No for the Smallest Possible

Hawking Radiation

Black holes can come in all sizes from about a billion tons up to billions of solar masses.

Because isolated black holes are difficult to detect, especially smaller mass ones, they have long been considered as candidates for dark matter, invoked to explain the extra gravitational accelerations measured at the outskirts of galaxies.

Stephen Hawking showed that black holes radiate low energy particles very slowly due to quantum thermodynamic effects. So the very lowest mass black holes evaporate away due to Hawking radiation during the life of the universe.

Voyager Satellites

The Voyager satellites were launched in 1977 and NASA has determined that Voyager 1 crossed the heliopause in 2012. This is the boundary for the solar wind, which holds back a large portion of galactic cosmic rays. Voyager 2 crossed the heliopause last year.

Forty-two years after launch, and having toured Jupiter, Saturn, Uranus, and Neptune, these remarkable satellites are still returning valuable data about the outer reaches of the Solar System.

What is the connection between black holes, dark matter, and Voyager 1?

In the early universe, large numbers of so-called primordial black holes (PBHs) of various sizes may have formed. The question arises, could these be the primary component of dark matter?

Primordial Black Holes as Dark Matter Candidates

The detection of gravitational waves from half a dozen mergers of black holes of intermediate mass has given new energy to this idea. Also, there is the continued failure to detect exotic particle candidates for dark matter in Earth-bound laboratory experiments.

A team of Japanese astronomers, searching for microlensing effects with stars in the Andromeda galaxy, have ruled out small black holes in the range of 10^{20} grams up to about 3 times the Earth’s mass. https://darkmatterdarkenergy.com/2017/12/07/primordial-black-holes-and-dark-matter has more detail.

Constraints from other lensing experiments (MACHO, EROS) and the cosmic microwave background appear to rule out more massive primordial black holes as the explanation for most dark matter.

What about the tiniest allowable black holes, from about 4 \cdot 10^{14} gm (smaller ones have evaporated already) up to 10^{20} gm?

Voyager 1 Constraints

With a recent analysis researchers at the Laboratoire de Physique Theorique et Hautes Energies (LPTHE) show that the Voyager 1 satellite now rules out primordial black holes with masses below 10^{17} gm as well, as the source of most dark matter. And it is because of the Hawking radiation that we do not detect.

Although Hawking radiation has never been detected, it is on very firm theoretical grounds that it should exist. Everything, including strange objects like black holes, has a quantum nature.

Smaller black holes radiate at higher temperatures and have shorter lifetimes. The Hawking radiation temperature is

T = 1.1  GeV / (m/10^{13} gm)

Thus for an m = 10^{16} gm black hole the Hawking temperature is about 1 MeV. (GeV or giga electron-Volt is a billion eV and around the rest mass energy of a proton, and an MeV or mega electron-Volt is a million eV and about twice the rest mass energy of an electron.)

Since these temperatures are in the MeV range, only very light particles such as neutrinos, electrons, and positrons would be emitted by the PBHs.

Figure 1 from the Boudaud and Cirelli paper shows the observed combined electron and positron cosmic ray flux from Voyager 1 in the energy range from 3 MeV to 50 MeV. It also shows results in the 1 to 10 GeV range from the Alpha Magnetic Spectrometer 2 experiment on the International Space Station (located well inside the heliopause). Two different models of how the energetic particles propagate through the galaxy are used.

Smallest possible Black Holes ruled out

PBHs with 10^{15} or 10^{16} grams are clearly ruled out; they would inject far too many energetic electron and positron cosmic rays into the interstellar medium that Voyager 1 has entered.

The authors state that no more than 0.1% of dark matter can be due to PBHs of mass less than 10^{16} grams (10 billion tons).

In Figure 1, a monotonic mass distribution was assumed (PBHs all have the same mass). They also consider various log-normal mass distributions and similar constraints on the allowable PBH mass were found.

What about at 10^{17} grams and above? Most mass regions are ruled out.

The mass region above 5 \cdot 10^{17} grams and up to about 10^{20} grams has been excluded as a primary source of dark matter from PBHs by a 2012* result from Barnacka, Glicenstein, and Moderski. They searched for gravitational lensing effects upon gamma ray burst sources due to intervening black holes.

So vast ranges of possible PBH masses are ruled out. However the mass region from 3 \cdot 10^{16} up to 5 \cdot 10^{17} grams remains a possibility as a dark matter hideout for PBHs.

*The same year that Voyager 1 crossed the heliopause, coincidentally

References

Boudaud, M. And Cirelli, M. 2019 “Voyager 1 electrons and positrons further constrain primordial black holes as dark matter” https://arxiv.org/abs/1807.03075

https://darkmatterdarkenergy.com/2017/12/07/primordial-black-holes-and-dark-matter/

Barnacka, A., Glicenstein, J.-F., Moderski, R. 2012 “New constraints on primordial black holes abundance from femtolensing of gamma-ray bursts” http://arxiv.org/abs/1204.2056

Leave a comment   |  tags: , , , , , , | posted in Dark Matter, primordial black holes

September 19, 2018

Matter and Energy Tell Spacetime How to Be: Dark Gravity

By Stephen Perrenod

Is gravity fundamental or emergent? Electromagnetism is one example of a fundamental force. Thermodynamics is an example of emergent, statistical behavior.

Newton saw gravity as a mysterious force acting at a distance between two objects, obeying the well-known inverse square law, and occurring in a spacetime that was inflexible, and had a single frame of reference.

Einstein looked into the nature of space and time and realized they are flexible. Yet general relativity is still a classical theory, without quantum behavior. And it presupposes a continuous fabric for space.

As John Wheeler said, “spacetime tells matter how to move; matter tells spacetime how to curve”. Now Wheeler full well knew that not just matter, but also energy, curves spacetime.

A modest suggestion: invert Wheeler’s sentence. And then generalize it. Matter, and energy, tells spacetime how to be.

Which is more fundamental? Matter or spacetime?

Quantum theories of gravity seek to couple the known quantum fields with gravity, and it is expected that at the extremely small Planck scales, time and space both lose their continuous nature.

In physics, space and time are typically assumed as continuous backdrops.

But what if space is not fundamental at all? What if time is not fundamental? It is not difficult to conceive of time as merely an ordering of events. But space and time are to some extent interchangeable, as Einstein showed with special relativity.

So what about space? Is it just us placing rulers between objects, between masses?

Particle physicists are increasingly coming to the view that space, and time, are emergent. Not fundamental.

If emergent, from what? The concept is that particles, and quantum fields, for that matter, are entangled with one another. Their microscopic quantum states are correlated. The phenomenon of quantum entanglement has been studied in the laboratory and is well proven.

Chinese scientists have even, just last year, demonstrated quantum entanglement of photons over a satellite uplink with a total path exceeding 1200 kilometers.

Quantum entanglement thus becomes the thread Nature uses to stitch together the fabric of space. And as the degree of quantum entanglement changes the local curvature of the fabric changes. As the curvature changes, matter follows different paths. And that is gravity in action.

Newton’s laws are an approximation of general relativity for the case of small accelerations. But if space is not a continuous fabric and results from quantum entanglement, then for very small accelerations (in a sub-Newtonian range) both Newton dynamics and general relativity may be incomplete.

The connection between gravity and thermodynamics has been around for four decades, through research on black holes, and from string theory. Jacob Bekenstein and Stephen Hawking determined that a black hole possesses entropy proportional to its area divided by the gravitational constant G. This area law entropy approach can be used to derive general relativity as Ted Jacobson did in 1995.

But it may be that the supposed area law component is insufficient; according to Erik Verlinde’s new emergent gravity hypothesis, there is also a volume law component for entropy, that must be considered due to dark energy and when accelerations are very low.

We have had hints about this incomplete description of gravity in the velocity measurements made at the outskirts of galaxies during the past eight decades. Higher velocities than expected are seen, reflecting higher acceleration of stars and gas than Newton (or Einstein) would predict. We can call this dark gravity.

Now this dark gravity could be due to dark matter. Or it could just be modified gravity, with extra gravity over what we expected.

It has been understood since the work of Mordehai Milgrom in the 1980s that the excess velocities that are observed are better correlated with extra acceleration than with distance from the galactic center.

Stacey McGaugh and collaborators have demonstrated a very tight correlation between the observed accelerations and the expected Newtonian acceleration, as I discussed in a prior blog here. The extra acceleration kicks in below a few times 10^{-10} meters per second per second (m/s²).

This is suspiciously close to the speed of light divided by the age of the universe! Which is about 7 \cdot 10^{-10} m/s².

Why should that be? The mass/energy density (both mass and energy contribute to gravity) of the universe is dominated today by dark energy.

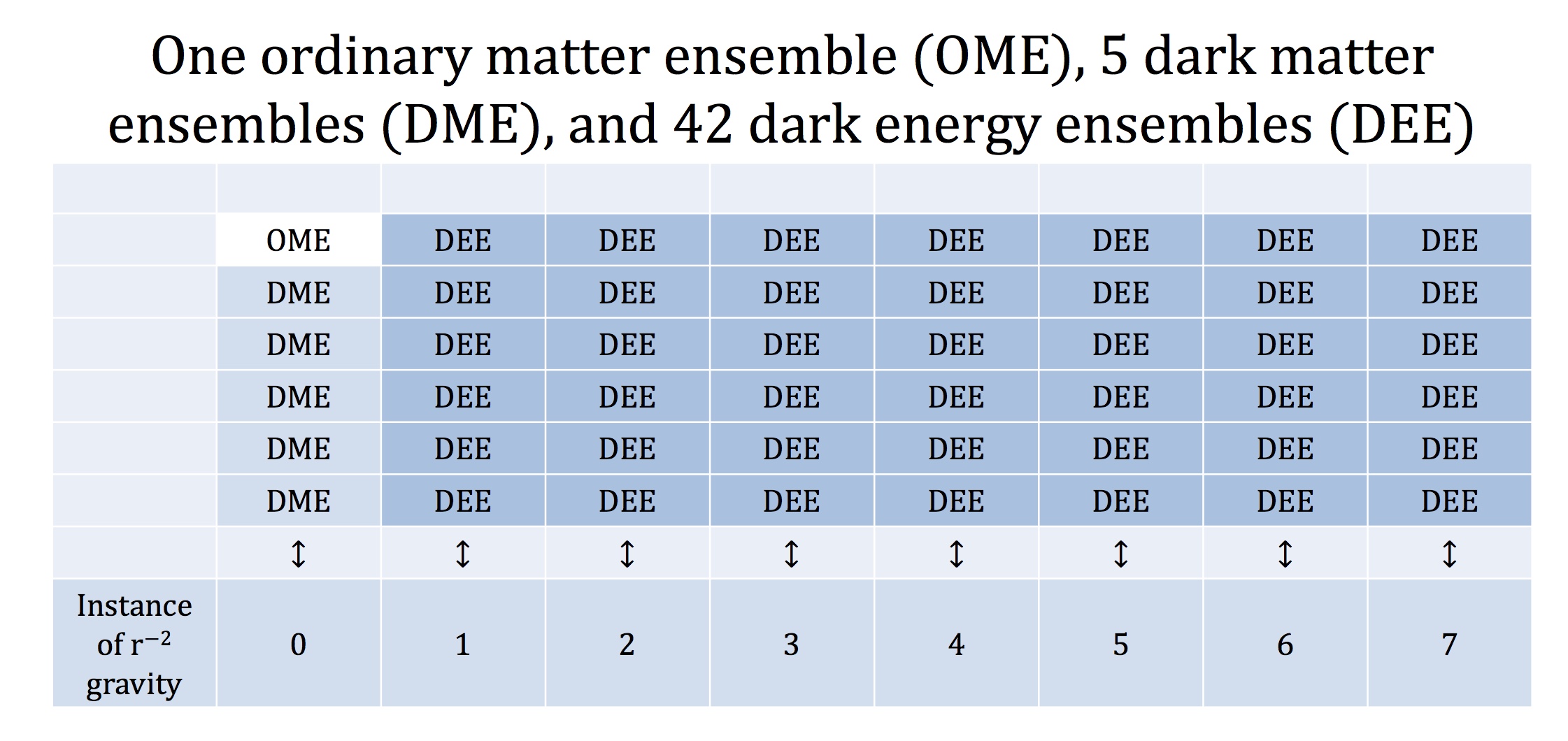
The canonical cosmological model has 70% dark energy, 25% dark matter, and 5% ordinary matter. In fact if there is no dark matter, just dark gravity, or dark acceleration, then it could be more like a 95% and 5% split between dark energy and (ordinary) matter components.

A homogeneous universe composed only of dark energy in general relativity is known as a de  Sitter (dS) universe. Our universe is, at present, basically a dS universe ‘salted’ with matter.

Then one needs to ask how does gravity behave in dark energy influenced domains? Now unlike ordinary matter, dark energy is highly uniformly distributed on the largest scales. It is driving an accelerated expansion of the universe (the fabric of spacetime!) and dragging the ordinary matter along with it.

But where the density of ordinary matter is high, dark energy is evacuated. An ironic thought, since dark energy is considered to be vacuum energy. But where there is lots of matter, the vacuum is pushed aside.

That general concept was what Erik Verlinde used to derive an extra acceleration formula in 2016. He modeled an emergent, entropic gravity due to ordinary matter and also due to the interplay between dark energy and ordinary matter.  He modeled the dark energy as responding like an elastic medium when it is displaced within the vicinity of matter. Using this analogy with elasticity, he derived an extra acceleration as proportional to the square root of the product of the usual Newtonian acceleration and a term related to the speed of light divided by the universe’s age. This leads to a 1/r force law for the extra component since Newtonian acceleration goes as 1/r².

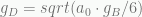
g _D = sqrt  {(a_0 \cdot g_B / 6 )}

Verlinde’s dark gravity depends on the square root of the product of a characteristic acceleration a0 and ordinary Newtonian (baryonic) gravity, gB

The idea is that the elastic, dark energy medium, relaxes over a cosmological timescales. Matter displaces energy and entropy from this medium, and there is a back reaction of the dark energy on matter that is expressed as a volume law entropy. Verlinde is able to show that this interplay between the matter and dark energy leads precisely to the characteristic acceleration is a_0 / 6 = c \cdot H / 6 , where H is the Hubble expansion parameter and is equal to one over the age of the universe for a dS universe. This turns out be the right value of just over 10^{-10} m/s² that matches observations.

In our solar system, and indeed in the central regions of galaxies, we see gravity as the interplay of ordinary matter and other ordinary matter. We are not used to this other dance.

Domains of gravity

Acceleration

 Domain Gravity vis-a-vis Newtonian formula

Examples
High (GM/R ~ c²) Einstein, general relativity Higher

Black holes, neutron stars
Normal Newtonian dynamics 1/r² Solar system, Sun orbit in Milky Way

Very low (< c/ age of U.)

 Dark Gravity Higher, additional 1/r term Outer edges of galaxies, dwarf galaxies, clusters of galaxies

The table above summarizes three domains for gravity: general relativity, Newtonian, and dark gravity, the latter arising at very low accelerations. We are always calculating gravity incorrectly! Usually, such as in our solar system, it matters not at all. For example at the Earth’s surface gravity is 11 orders of magnitude greater than the very low acceleration domain where the extra term kicks in.

Recently, Alexander Peach, a Teaching Fellow in physics at Durham University, has taken a different angle based on Verlinde’s original, and much simpler, exposition of his emergent gravity theory in his 2010 paper. He derives an equivalent result to Verlinde’s in a way which I believe is easier to understand. He assumes that holography (the assumption that all of the entropy can be calculated as area law entropy on a spherical screen surrounding the mass) breaks down at a certain length scale. To mimic the effect of dark energy in Verlinde’s new hypothesis, Peach adds a volume law contribution to entropy which competes with the holographic area law at this certain length scale. And he ends up with the same result, an extra 1/r entropic force that should be added for correctness in very low acceleration domains.

Peach.fig2.jpeg

In figure 2 (above) from Peach’s paper he discusses a test particle located beyond a critical radius r_c for which volume law entropy must also be considered. Well within r_c  (shown in b) the dark energy is fully displaced by the attracting mass located at the origin and the area law entropy calculation is accurate (indicated by the shaded surface). Beyond r_c the dark energy effect is important, the holographic screen approximation breaks down, and the volume entropy must be included in the contribution to the emergent gravitational force (shown in c). It is this volume entropy that provides an additional 1/r term for the gravitational force.

Peach makes the assumption that the bulk and boundary systems are in thermal equilibrium. The bulk is the source of volume entropy. In his thought experiment he models a single bit of information corresponding to the test particle being one Compton wavelength away from the screen, just as Verlinde initially did in his description of emergent Newtonian gravity in 2010. The Compton wavelength is equal to the wavelength a photon would have if its energy were equal to the rest mass energy of the test particle. It quantifies the limitation in measuring the position of a particle.

Then the change in boundary (screen) entropy can be related to the small displacement of the particle. Assuming thermal equilibrium and equipartition within each system and adopting the first law of thermodynamics, the extra entropic force can be determined as equal to the Newtonian formula, but replacing one of the r terms in the denominator by r_c .

To understand r_c , for a given system, it is the radius at which the extra gravity is equal to the Newtonian calculation, in other words, gravity is just twice as strong as would be expected at that location. In turn, this traces back to the fact that, by definition, it is the length scale beyond which the volume law term overwhelms the holographic area law.

It is thus the distance at which the Newtonian gravity alone drops to about 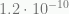1.2 \cdot 10^{-10} m/s², i.e. c \cdot H / 6 , for a given system.

So Peach and Verlinde use two different methods but with consistent assumptions to model a dark gravity term which follows a 1/r force law. And this kicks in at around 10^{-10} m/s².

The ingredients introduced by Peach’s setup may be sufficient to derive a covariant theory, which would entail a modified version of general relativity that introduces new fields, which could have novel interactions with ordinary matter. This could add more detail to the story of covariant emergent gravity already considered by Hossenfelder (2017), and allow for further phenomenological testing of emergent dark gravity. Currently, it is not clear what the extra degrees of freedom in the covariant version of Peach’s model should look like. It may be that Verlinde’s introduction of elastic variables is the only sensible option, or it could be one of several consistent choices.

With Peach’s work, physicists have taken another step in understanding and modeling dark gravity in a fashion that obviates the need for dark matter to explain our universe

We close with another of John Wheeler’s sayings:

“The only thing harder to understand than a law of statistical origin would be a law that is not of statistical origin, for then there would be no way for it—or its progenitor principles—to come into being. On the other hand, when we view each of the laws of physics—and no laws are more magnificent in scope or better tested—as at bottom statistical in character, then we are at last able to forego the idea of a law that endures from everlasting to everlasting. “

It is a pleasure to thank Alexander Peach for his comments on, and contributions to, this article.

References:

https://darkmatterdarkenergy.com/2018/08/02/dark-acceleration-the-acceleration-discrepancy/ blog “Dark Acceleration: The Acceleration Discrepancy”

https://arxiv.org/abs/gr-qc/9504004 “Thermodynamics of Spacetime: The Einstein Equation of State” 1995, Ted Jacobson

https://darkmatterdarkenergy.com/2017/07/13/dark-energy-and-the-comological-constant/ blog “Dark Energy and the Cosmological Constant”

https://darkmatterdarkenergy.com/2016/12/30/emergent-gravity-verlindes-proposal/ blog “Emergent Gravity: Verlinde’s Proposal”

https://arxiv.org/pdf/1806.10195.pdf “Emergent Dark Gravity from (Non) Holographic Screens” 2018, Alexander Peach

https://arxiv.org/pdf/1703.01415.pdf “A Covariant Version of Verlinde’s Emergent Gravity” Sabine Hossenfelder

1 Comment   |  tags: , , , , , , , | posted in Dark Energy, Dark Matter, Gravity

June 26, 2018

WIMPZillas: The Biggest WIMPs

By Stephen Perrenod

Godzilla_1954-2014_incarnations.jpg

In the search for direct detection of dark matter, the experimental focus has been on WIMPS – weakly interacting massive particles. Large crystal detectors are placed deep underground to avoid contamination from cosmic rays and other stray particles.

WIMPs are often hypothesized to arise as supersymmetric partners of Standard Model particles. However, there are also WIMP candidates that arise due to non-supersymmetric extensions to the Standard Model.

The idea is that the least massive supersymmetric particle would be stable, and neutral. The (hypothetical) neutralino is the most often cited candidate.

The search technique is essentially to look for direct recoil of dark matter particles onto ordinary atomic nuclei.

The only problem is that we keep not seeing WIMPs. Not in the dark matter searches, not at the Large Hadron Collider whose main achievement has been the detection of the Higgs boson at mass 125 GeV. The mass of the Higgs is somewhat on the heavy side, and constrains the likelihood of supersymmetry being a correct Standard Model extension.

The figure below shows WIMP interaction with ordinary nuclear matter cross-section limits from a range of experiments spanning from 1 to 1000 GeV masses for WIMP candidates. Typical supersymmetric (SUSY) models are disfavored by these results at higher masses above 40 GeV or so as the observational limits are well down into the yellow shaded regions.

WIMPLimits

Perhaps the problem is that the WIMPs are much heavier than where the experiments have been searching. Most of the direction detection experiments are sensitive to candidate masses in the range from around 1 GeV to 1000 GeV (1 GeV or giga-electronVolt is about 6% greater than the rest mass energy of a proton). The 10 to 100 GeV range has been the most thoroughly searched region and multiple experiments place very strong constraints on interaction cross-sections with normal matter.

WIMPzillas is the moniker given to the most massive WIMPs, with masses from a billion GeV up to  potentially as large as the GUT (grand Unified Theory) scale of 10^{16}    GeV .

The more general term is Superheavy Dark Matter, and this is proposed as a possibility for unexplained ultra high energy cosmic rays (UHECR). The WIMPzillas may decay to highly energetic gamma rays, or other particles, and these would be detected as the UHECR. 

UHECR have energies greater than a billion GeV (10^9 GeV) and the most massive event ever seen (the so-called Oh My God Particle) was detected at 3 \cdot 10^{11}  GeV . It had energy equivalent to a baseball with velocity of 94 kilometers per hour. Or 40 million times the energy of particles in the Large Hadron Collider.

It has taken decades of searching at multiple cosmic ray arrays to detect particles at or near that energy.

Most UHECR appear to be spatially correlated with external galaxy sources, in particular with nearby Active Galactic Nuclei that are powered by supermassive black holes accelerating material near, but outside of, their event horizons.

However, they are not expected to be able to produce cosmic rays with energies above around 10^{11} GeV , thus the WIMPzilla possibility. Again WIMPzillas could span the range from 10^9 GeV up to 10^{16} GeV .

In a paper published last year, Kolb and Long calculated the production of WIMPzillas from Higgs boson pairs in the early universe. These Higgs pairs would have very high kinetic energies, much beyond their rest mass.

This production would occur during the “Reheating” period after inflation, as the inflaton (scalar energy field) dumped its energy into particles and radiation of the plasma.

There is another production mechanism, a gravitational mechanism, as the universe transitions from the accelerated expansion phase during cosmological inflation into the matter dominated (and then radiation-dominated) phases.

Thermal production from the Higgs portal, according to their results, is the dominant source of WIMPzillas for masses above 10^{14} GeV . It may also be the dominant source for masses less than about 10^{11} GeV .

They based their assumptions on chaotic inflation with quadratic inflation potential, followed by a typical model for reheating, but do not expect that their conclusions would be changed strongly with different inflation models.

It will take decades to discriminate between Big Bang-produced WIMPzilla style cosmic rays and those from extragalactic sources, since many more 10^{11} GeV  and above UHECRs should be detected to build statistics on these rare events.

But it is possible that WIMPzillas have already been seen.

The density is tiny. The current dark matter density in the Solar neighborhood is measured at 0.4 Gev per cc. Thus in a cubic meter there would be the equivalent of 400,000 proton masses. 

But if the WIMPzillas are at energies 10^{11} Gev and above (100 billion GeV), a cubic kilometer would only contain 4000 particles at a given time. Not easy to catch.

References

http://cdms.berkeley.edu/publications.html – SuperCDMS experiment led by UC Berkeley

http://pdg.lbl.gov/2017/reviews/rpp2017-rev-dark-matter.pdf – Dark matter review chapter from Lawrence Berkeley Lab (Figure above is from this review article).

http://home.physics.ucla.edu/~arisaka/home3/Particle/Cosmic_Rays/ – Ultra high energy cosmic rays

https://arxiv.org/pdf/1708.04293.pdf – E. Kolb and A. Long, 2017 “Superheavy Dark Matter through Higgs Portal Operators”

2 Comments   |  tags: , , , , , | posted in Dark Matter

March 4, 2018

Dark Ages, Dark Matter

By Stephen Perrenod

Cosmologists call the first couple of hundred million years of the universe’s history the Dark Ages. This is the period until the first stars formed. The Cosmic Dawn is the name given to the epoch during which these first stars formed.

Now there has been a stunning detection of the 21 centimeter line from neutral hydrogen gas in that era. Because the first stars are beginning to form, their radiation induces the hyperfine transition for electrons in the ground state orbitals of hydrogen. This radiation undergoes a cosmological expansion of around a factor of 18 since the era of the Cosmic Dawn. By the time it reaches us, instead of being at the laboratory frequency of 1420 MHz, it is at around 78 MHz.

This is a difficult frequency at which to observe, since the region of spectrum is between the TV and FM bands in the U.S. and instrumentation itself is a source of radio noise. Very remote, radio quiet, sites are necessary to minimize interference from terrestrial sources, and the signal must be picked out from a much stronger cosmic background.

EDGES-2.jpg

 

Image credit: CSIRO-Australia and EDGES collaboration, MIT and Arizona State University. EDGES is funded by the National Science Foundation.

This detection was made in Western Australia with a radio detector known as EDGES, that is sensitive in the 50 to 100 MHz range. It is surprisingly small, roughly the size of a large desk. The EDGES program is a collaboration between MIT and Arizona State University.

The researchers detected an absorption feature beginning at 78 MHz, corresponding to a redshift of 17.2 (1420/78 = 18.2 = 1 + z, where z is redshift) and for  the canonical cosmological model it corresponds to an age of the universe of 180 million years.

The absorption feature is much stronger than expected from models, implying a lower gas temperature than expected.

At that redshift the cosmic microwave background temperature is at 50 Kelvins (at the present era it is only 2.7 Kelvins). The neutral hydrogen feature is seen in absorption against the warmer cosmic microwave background, and is much cooler (both its ‘spin’ and ‘kinetic’ temperatures).

This neutral hydrogen appears to be at only 3 Kelvins. Existing models had the expectation that it would be at around 7 Kelvins or even higher. (A Kelvin degree equals a Celsius degree, but has its zero point at absolute zero rather than water’s freezing temperature).

In a companion paper, it has been proposed that interactions with dark matter kept the hydrogen gas cooler than expected. This would require an interaction cross section between dark matter and ordinary matter (non- gravitational interaction, perhaps due to the weak force) and low velocities and low masses for dark matter particles. The mass should be only a few GeV (a proton rest mass is .94 GeV). Most WIMP searches in Earth-based labs have been above 10 GeV.

These results need to be confirmed by other experiments. And the dark matter explanation is speculative. But the door has been opened for Cosmic Dawn observations of neutral hydrogen as a new way to hunt for dark matter.

References:

“A Surprising Chill before the Cosmic Dawn” https://www.nature.com/articles/d41586-018-02310-9

EDGES science: http://loco.lab.asu.edu/edges/edges-science/

EDGES array and program: https://www.haystack.mit.edu/ast/arrays/Edges/

R. Barkana 2018, “Possible Interactions between Baryons and Dark Matter Particles Revealed by the First Stars” http://www.nature.com/articles/nature25791

1 Comment   |  tags: , , , , , | posted in Dark Matter, Early Universe

February 11, 2018

Unified Physics including Dark Matter and Dark Energy

By Stephen Perrenod

Dark matter keeps escaping direct detection, whether it might be in the form of WIMPs, or primordial black holes, or axions. Perhaps it is a phantom and general relativity is inaccurate for very low accelerations. Or perhaps we need a new framework for particle physics other than what the Standard Model and supersymmetry provide.

We are pleased to present a guest post from Dr. Thomas J. Buckholtz. He introduces us to a theoretical framework referred to as CUSP, that results in four dozen sets of elementary particles. Only one of these sets is ordinary matter, and the framework appears to reproduce the known fundamental particles. CUSP posits ensembles that we call dark matter and dark energy. In particular, it results in the approximate 5:1 ratio observed for the density of dark matter relative to ordinary matter at the scales of galaxies and clusters of galaxies. (If interested, after reading this post, you can read more at his blog linked to his name just below).

Thomas J. Buckholtz

My research suggests descriptions for dark matter, dark energy, and other phenomena. The work suggests explanations for ratios of dark matter density to ordinary matter density and for other observations. I would like to thank Stephen Perrenod for providing this opportunity to discuss the work. I use the term CUSP – concepts uniting some physics – to refer to the work. (A book, Some Physics United: With Predictions and Models for Much, provides details.)

CUSP suggests that the universe includes 48 sets of elementary-particle Standard Model elementary particles and composite particles. (Known composite particles include the proton and neutron.) The sets are essentially (for purposes of this blog) identical. I call each instance an ensemble. Each ensemble includes its own photon, Higgs boson, electron, proton, and so forth. Elementary particle masses do not vary by ensemble. (Weak interaction handedness might vary by ensemble.)

One ensemble correlates with ordinary matter, 5 ensembles correlate with dark matter, and 42 ensembles contribute to dark energy densities. CUSP suggests interactions via which people might be able to detect directly (as opposed to infer indirectly) dark matter ensemble elementary particles or composite particles. (One such interaction theoretically correlates directly with Larmor precession but not as directly with charge or nominal magnetic dipole moment. I welcome the prospect that people will estimate when, if not now, experimental techniques might have adequate sensitivity to make such detections.)

Buckholtztable

This explanation may describe (much of) dark matter and explain (at least approximately some) ratios of dark matter density to ordinary matter density. You may be curious as to how I arrive at suggestions CUSP makes. (In addition, there are some subtleties.)

Historically regarding astrophysics, the progression ‘motion to forces to objects’ pertains. For example, Kepler’s work replaced epicycles with ellipses before Newton suggested gravity. CUSP takes a somewhat reverse path. CUSP models elementary particles and forces before considering motion. The work regarding particles and forces matches known elementary particles and forces and extrapolates to predict other elementary particles and forces. (In case you are curious, the mathematics basis features solutions to equations featuring isotropic pairs of isotropic quantum harmonic oscillators.)

I (in effect) add motion by extending CUSP to embrace symmetries associated with special relativity. In traditional physics, each of conservation of angular momentum, conservation of momentum, and boost correlates with a spatial symmetry correlating with the mathematics group SU(2). (If you would like to learn more, search online for “conservation law symmetry,” “Noether’s theorem,” “special unitary group,” and “Poincare group.”) CUSP modeling principles point to a need to add to temporal symmetry and, thereby, to extend a symmetry correlating with conservation of energy to correlate with the group SU(7). The number of generators of a group SU(n) is n2−1. SU(7) has 48 generators. CUSP suggests that each SU(7) generator correlates with a unique ensemble. (In case you are curious, the number 48 pertains also for modeling based on either Newtonian physics or general relativity.)

CUSP math suggests that the universe includes 8 (not 1 and not 48) instances of traditional gravity. Each instance of gravity interacts with 6 ensembles.

The ensemble correlating with people (and with all things people see) connects, via our instance of gravity, with 5 other ensembles. CUSP proposes a definitive concept – stuff made from any of those 5 ensembles – for (much of) dark matter and explains (approximately) ratios of dark matter density to ordinary matter density for the universe and for galaxy clusters. (Let me not herein do more than allude to other inferably dark matter based on CUSP-predicted ordinary matter ensemble composite particles; to observations that suggest that, for some galaxies, the dark matter to ordinary matter ratio is about 4 to 1, not 5 to 1; and other related phenomena with which CUSP seems to comport.)

CUSP suggests that interactions between dark matter plus ordinary matter and the seven peer combinations, each comprised of 1 instance of gravity and 6 ensembles, is non-zero but small. Inferred ratios of density of dark energy to density of dark matter plus ordinary matter ‘grow’ from zero for observations pertaining to somewhat after the big bang to 2+ for observations pertaining to approximately now. CUSP comports with such ‘growth.’ (In case you are curious, CUSP provides a nearly completely separate explanation for dark energy forces that govern the rate of expansion of the universe.)

Relationships between ensembles are reciprocal. For each of two different ensembles, the second ensemble is either part of the first ensemble’s dark matter or part of the first ensemble’s dark energy. Look around you. See what you see. Assuming that non-ordinary-matter ensembles include adequately physics-savvy beings, you are looking at someone else’s dark matter and yet someone else’s dark energy stuff. Assuming these aspects of CUSP comport with nature, people might say that dark matter and dark-energy stuff are, in effect, quite familiar.

Copyright © 2018 Thomas J. Buckholtz

 

1 Comment   |  tags: , , , , , , , | posted in Dark Energy, Dark Matter

December 7, 2017

Primordial Black Holes and Dark Matter

By Stephen Perrenod

Based on observed gravitational interactions in galactic halos (galaxy rotation curves) and in group and clusters, there appears to be 5 times as much dark matter as ordinary matter in the universe. The alternative is no dark matter, but more gravity than expected at low accelerations, as discussed in this post on emergent gravity.

The main candidates for dark matter are exotic, undiscovered particles such as WIMPs (weakly interacting massive particles) and axions. Experiments attempting direct detection for these have repeatedly come up short.

The non-particle alternative category is MACHOs (massive compact halo objects) composed of ordinary matter.  Planets, dwarf stars and neutron stars have been ruled out by various observational signatures. The one ordinary matter possibility that has remained viable is that of black holes, and in particular black holes with much less than the mass of the Sun.

The only known possibility for such low mass black holes is that of primordial black holes (PBHs) formed in the earliest moments of the Big Bang.

Gravitational microlensing, or microlensing for short, seeks to detect PBHs by their general relativistic gravitational effect on starlight. MACHO and EROS were experiments to monitor stars in the Large Magellanic Cloud. These were able to place limits on the abundance of PBHs with masses from about one hundred millionth of a the Sun’s mass up to 10 solar masses. PBHs from that mass range are not able to explain the total amount of dark matter determined from gravitational interactions.

LIGO has recently detected several merging black holes in the tens of solar mass range. However the frequency of LIGO detections appears too low by two orders of magnitude to explain the amount of gravitationally detected dark matter. PBHs in this mass range are also constrained by cosmic microwave background observations.

Extremely low mass PBHs, below 10 billion tons, cannot survive until the present epoch of the universe. This is due to Hawking radiation. Black holes evaporate due to their quantum nature. Solar mass black holes have an extremely long lifetime against evaporation. But very low mass black holes will evaporate in billions of years or much sooner, depending on mass.

The remaining mass window for possible PBH, in sufficient amount to explain dark matter, is from about 10 trillion ton objects up to those with ten millionths of the Sun’s mass.

MicrolensingPBHAndromeda

Figure 5 from H. Niikura et al. “Microlensing constraints on primordial black holes with the Subaru/HSC Andromeda observation”, https://arxiv.org/abs/1701.02151  

Here f is the fraction of dark matter which can be explained by PBHs. The red shaded area is excluded by the authors observations and analysis of Andromeda Galaxy data. This rules out masses above 100 trillion tons and below a hundred thousandth of the Sun’s mass. (Solar mass units used above and grams are used below).

 

Now, a team of Japanese astronomers have used the Subaru telescope on the Big Island of Hawaii (operated by Japan’s national observatory) to determine constraints on PBHs by observing millions of stars in the Andromeda Galaxy.

The idea is that a candidate PBH would pass in front of the line of sight to the star, acting as a lens, and magnifying the light from the star in question for a relatively brief period of time. The astronomers looked for stars exhibiting variability in their light intensity.

With only a single nights’ data they made repeated short exposures and were able to pick out over 15,000 stars in Andromeda exhibiting such variable light intensity. However, among these possible candidates, only a single one turned out to fit the characteristics expected for a PBH detection.

If PBHs in this mass range were sufficiently abundant to explain dark matter, then one would have expected of order one thousand events, and they saw nothing like this number. In summary, with 95% confidence, they are able to rule out PBHs as the main source of dark matter for the mass range from 100 trillion tons up to one hundred thousandth of the Sun’s mass.

The window for primordial black holes as the explanation for dark matter appears to be closing.

 

 

 

 

2 Comments   |  tags: , , , , | posted in Dark Energy, primordial black holes