Previously I have written about the possibility of primordial black holes as the explanation for dark matter, and on the observational constraints around such a possibility.
But maybe it is dark energy, not dark matter, that black holes explain. More precisely, it would be dark energy stars (or gravatars, or GEODEs) that are observationally similar to black holes.
Dark energy
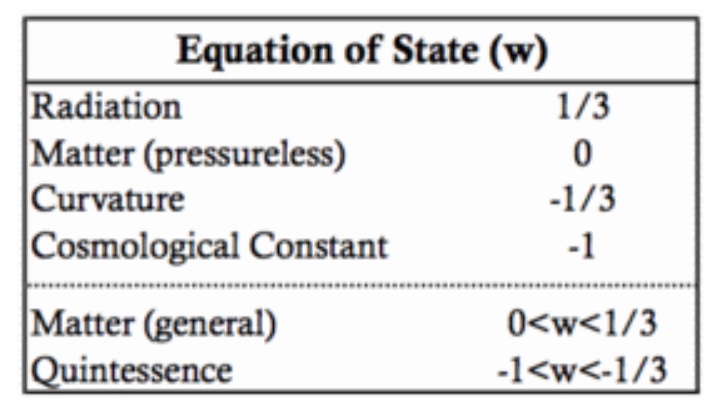
Dark energy is named thusly because it has negative pressure. There is something known as an equation of state that relates pressure to energy density. For normal matter, or for dark matter, the coefficient of the relationship, w, is zero or slightly positive, and for radiation it is 1/3.
If it is non-zero and positive then the fluid component loses energy as the universe expands, and for radiation, this means there is a cosmological redshift. The redshift is in proportion to the universe’s linear scale factor, which can be written as the inverse of the cosmological redshift plus one, by normalizing it to the present-day scale. The cosmological redshift is a measure of the epoch as well, currently z = 0, and the higher the redshift the farther we look back into the past, into the earlier years of the universe. Light emitted at frequency ν is shifted to lower frequency (longer wavelength) ν’ = ν / (1 + z).
Since 1998, we have known that we live in a universe dominated by dark energy (and its associated dark pressure, or negative pressure). The associated dark pressure outweighs dark energy by a factor of 3 because it appears 3 times, once for each spatial component in Einstein’s stress-energy tensor equations of general relativity.
Thus dark energy contributes a negative gravity, or expansion acceleration, and we observe that our universe has been accelerating in its expansion for the past 4 or 5 billion years, since dark energy now provides over 2/3 of the universal energy balance. Dark matter and ordinary matter together amount to just less than 1/3 of the average rest-mass energy density.
If w is less than -1/3 for some pervasive cosmological component, then you have dark energy behavior for that component, and in our universe today over the past several billion years, measurements show w = -1 or very close to it. This is the cosmological constant case where dark energy’s negative pressure has the same magnitude but the opposite sign of the positive dark energy density. More precisely, the dark pressure is the negative of the energy density times the speed of light squared.
Non-singular black holes
There has been consideration for decades of other types of black holes that would not have a singularity at the center. In standard solutions of general relativity black holes have a central singular point or flat zone, depending on whether their angular momentum is zero or positive.
For example a collapsing neutron star overwhelms all pressure support from neutron degeneracy pressure once its mass exceeds the TOV limit at about 2.7 solar masses (depending on angular momentum), and forms a black hole that is often presumed to collapse to a singularity.
But when considering quantum gravity, and quantum physics generally, then there should be some very exotic behavior at the center, we just don’t know what. Vacuum energy is one possibility.
For decades various proposals have been made for alternatives to a singularity, but the problem has been observationally intractable. A Soviet cosmologist Gliner, who was born just 100 years ago in Kyiv, and who only passed away in 2021, proposed the basis for dark energy stars and a dark energy driven cosmology framework in 1965 (in English translation, 1966).

E. Gliner, early 1970s in St. Petersburg, courtesy Gliner family
He defended his Ph.D. thesis in general relativity including dark energy as a component of the stress-energy tensor in 1972. Gliner emigrated to the US in 1980.
The essential idea is that the equation of state for compressed matter changes to that of a material (or “stuff”) with a fully negative pressure, w = -1 and thus that black hole collapse would naturally result in dark energy cores, creating dark energy stars or gravatars rather than traditional black holes. The cores could be surrounded with an intermediate transition zone and a skin or shell of normal matter (Beltracchi and Gondolo 2019). The dark energy cores would have negative pressure.
Standard black hole solution is incomplete
Normally black hole physics is attacked with Kerr (non-zero angular momentum) or Schwarzschild (zero angular momentum) solutions. But these are incomplete, in that they assume empty surroundings. There is no matching of the solution to the overall background which is a cosmological solution. The universe tracks an isotropic and homogeneous (on the largest scales) Lambda-cold dark matter (ΛCDM) solution of the equations of general relativity. Since dark energy now dominates, it is approaching a de Sitter exponential runaway, whereas traditional black hole solutions with singularities are quite the opposite, known as anti-de Sitter.
We have no general solution for black hole equations including the backdrop of an expanding universe. The local Kerr solution for rotating black holes that is widely used ignores the far field. Really one should match the two solution regimes, but there has been no analytical solution that does that; black hole computations are very difficult in general, even ignoring the far field.
In 2019, Croker and Weiner of the University of Hawaii found a way to match a model of dark energy cores to the standard ΛCDM cosmology, and demonstrate that for w = -1 that dark energy stars (black holes with dark energy cores) would have masses that grow in proportion to the cube of the universe’s linear scale factora, starting immediately from their initial formation at high redshifts. In effect they are forced to grow their masses and expand (with their radius proportional to mass as for a black hole) by all of the other dark energy stars in the universe acting in a collective fashion. They call this effect, cosmological coupling of the dark energy star gravity to the long-range and long-term cosmological gravitational field.
This can be considered a blueshift for mass, as distinguished from the energy or frequency redshift we see with radiation in the cosmos.
Their approach potentially addresses several problems: (1) an excess of larger galaxies and their supermassive black holes seen very early on in the recent James Webb Space Telescope data, (2) more intermediate mass black holes than expected, as confirmed from gravitational wave observations of black hole mergers, (see Coker, Zevin et al. 2021 for a possible explanation via cosmological coupling), and (3) possibly a natural explanation for all or a substantial portion of the dark energy in the universe, which has been assumed to be highly diffuse rather than composed primarily of a very large number of point sources.
Inside dark energy stars, the dark energy density would be many, many orders of magnitude higher than it is in the universe at large. But as we will see below, it might be enough to explain all of the dark energy budget of the ΛCDM cosmology.

M87* supermassive black hole (or dark energy star) imaged in polarized radio waves by the Event Horizon Telescope collaboration; signals are combined from a global collection of radio telescopes via aperture synthesis techniques. European Southern Observatory, licensed under a Creative Commons Attribution 4.0 International License
A revolutionary proposal
Here’s where it gets weird. A number of researchers have investigated the coupling of a black hole’s interior to an external expanding universe. In this case there is no singularity but instead a vacuum energy solution interior to the (growing) compact stellar remnant.
And one of the most favored possibilities is that the coupling causes the mass for all black holes to grow in proportion to the universe’s characteristic linear size a cubed, just as if it were a cosmological constant form of dark energy. This type of “stuff” retains equal energy density throughout all of space even as the space expands, as a result of its negative pressure with equation of state parameter w = -1.
Just this February a very interesting pair of papers has been published in The Astrophysical Journal (the most prestigious American journal for such work) by a team of astronomers from 9 countries (US, UK, Canada, Japan, Netherlands, Germany, Denmark, Portugal, and Cyprus), led by the University of Hawaii team mentioned above.
They have used observations of a large number of supermassive black holes and their companion galaxies out to redshift 2.5 (when the universe was less than 3 billion years of age) to argue that there is observable cosmologicalcouplingbetween the cosmological gravitational field at large and the SMBH masses, where they suppose those masses are dominated by dark energy cores.
Their argument is that the black hole* (or *dark energy star) masses have grown much faster than could be explained by the usual mechanism of accretion of nearby matter and mergers.
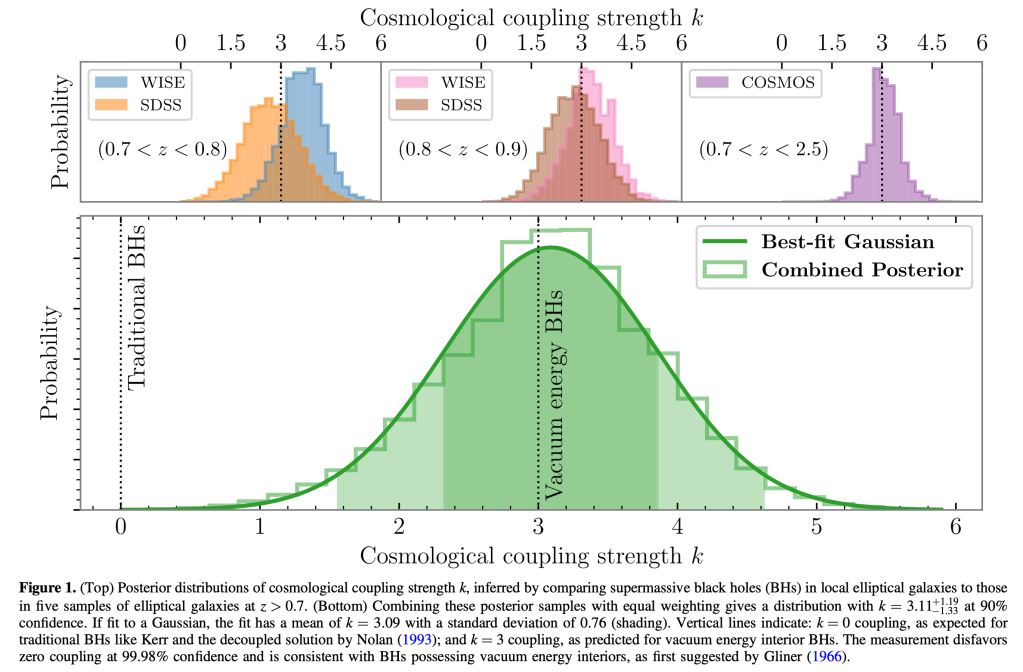
In Figure 1 from their second paper of the pair (Farrah, Croker, et al. 2023), they present their measurements of the strength of cosmological coupling for five different galaxy surveys (three sets of galaxies but two sets were surveyed at two frequencies each). They observed strong increases in the measured SMBH masses from redshifts close to z =1 and extending above z = 2. They derive a coupling strength parameter k that measures the power law index of how fast the black hole masses grow with redshift.
Their reformulation of the black hole model to include the far field yields cosmological coupling of the dark energy cores. The mass of the dark energy core, coupled to the overall cosmological solution, results in a mass increase M ~ a^k , a power law of index k, depending on the equation of state for the dark energy. Here a is the cosmological linear scale factor of the universal expansion and is also equal to 1/(1+z) where z is the redshift at which a galaxy and its SMBH are observed. (The scale factor a is normalized to 1 presently, such that z = 0 now and is positive in the past).
And they are claiming that their sample of several hundred galaxies and supermassive black holes indicates k = 3, on average, more or less. So between z = 1 and z = 0, over the past 8 billion years, they interpret their observations as an 8-fold growth in black hole masses. And they say this is consistent with M growing by a^3 as the universe’s linear scale has doubled (a was 1/2 at z = 1). This implies they are measuring a different class of black holes than we normally think of, those don’t increase in mass other than by accretion and mergers. Normal black holes would yield k > 0 but not by much, based on expected accretion and mergers. The k = 0 case they state is excluded by their observations with over 99.9% confidence.
The set of upper graphs in Figure 1 is for the various surveys, and the large lower graph combines all of the surveys as a single data set. They find a near-Gaussian distribution, and k is centered near 3, with an uncertainty close to 1. There is a 2/3 chance that the value lies between 2.33 and 3.85, based on their total sample of over 400 active galaxy nuclei.
And they also suggest this effect would be for all dark energy dominated “black holes”, including stellar class and intermediate BHs, not just SMBHs. So they claim fast evolution in all dark energy star masses, in proportion to the volume growth of the expanding universe, and consistent with dark energy cores having an equation of state just like the observed cosmological constant.
Now it gets really interesting.
We already know that the dark energy density of the universe, unlike the ever-thinning mater and radiation density, is more or less constant in absolute terms. That is the cosmological constant, due to vacuumenergy, interpretation of dark energy for which the pressure is negative and causes acceleration of the universe’s expansion. Each additional volume of the growth has its own associated vacuum energy (around 4 proton masses’ worth of rest energy per cubic meter). This is the universe’s biggest free lunch since its original creation.
The authors focus on dark energy starts created during the earliest bursts of star formation. These are the so-called Pop III stars, never observed because all or mostly all have reached end of life long ago. When galaxy and star formation starts as early as about 200 million years after the Big Bang, there is only hydrogen and helium for atomic matter. Heavier elements must be made in those first Pop III stars. As a result of their composition, the first stars with zero ‘metallacity’ have higher stellar masses; high mass stars are the ones that evolve most rapidly and they quickly end up as white dwarfs, or more to the point here, black holes or neutron stars in supernovae events. Or, they end their lives as dark energy stars.
The number of these compact post supernova remnant stars will decrease in density in inverse proportion to the increasing volume of the expanding universe. But the masses of all those that are dark energy stars would increase as the cube of the scale factor, in proportion to the increasing volume.
And the net effect would be just right to create a cosmological constant form of dark energy as the total contribution of billions upon billions of dark energy stars. And dark energy would be growing as a background field from very early on. Regular matter and dark matter thin out with time, but this cohort would have roughly constant energy density once most of the first early rounds of star formation completed, perhaps by redshift z = 8, well within the first billion years. Consequently, dark energy cores, collectively, would dominate the universe within the last 4 or 5 billion years or so, as the ordinary and dark matter density fell off. And now its dominance keeps growing with time.
But is there enough dark energy in cores?
But is it enough? How much dark energy is captured in these dark energy stars, and can it explain the dominant 69% of the universe’s energy balance that is inferred from observations of distant supernovae, and from other methods?
The dark energy cores are presumably formed from the infall and extreme compression of ordinary matter, from baryons captured into the progenitors of these black hole like stars and being compressed to such a high degree that they are converted into a rather uniform dark energy fluid. And that dark energy fluid has the unusual property of negative pressure that prevents further compression to a singularity.
It is possible they could consume some dark matter, but ordinary matter clumps much more easily since it can radiate away energy via radiation, which dark matter does not do. Any dark matter consumption would only build their case here, but we know the overall dark matter ratio of 5:1 versus ordinary matter has not changed much since the cosmic microwave background emission after the first 380,000 years.
We know from cosmic microwave background measurements and other observations, that the ordinary matter or baryon budget of the universe is just about 4.9%, we’ll call it 5% in round numbers. The rest is 69% dark energy, and 26% dark matter.
So the question is, how much of the 5% must be locked up in dark energy stars to explain the 69% dark energy dominance that we currently see?
Remember that with dark energy stars the mass grows as the volume of the universe grows, that is in proportion to (1 + z)3. Now dark energy stars will be formed at different cosmological redshifts, but let’s just ask what fraction of baryons would we need to convert, assuming all are formed at the same epoch. This will give us a rough feel for the range of when and of how much.
Table 1 looks at some possibilities. It asks what fraction of baryons need to collapse into dark energy cores, and we see that the range is from only about 0.2% to 1% of baryons are required. Those baryons are just 5% of the mass-energy of the universe, and only 1% or less of those are needed, because the mass expansion factors range from about 1000 to about 10,000 — 3 to 4 orders of magnitude, depending on when the dark energy stars form.
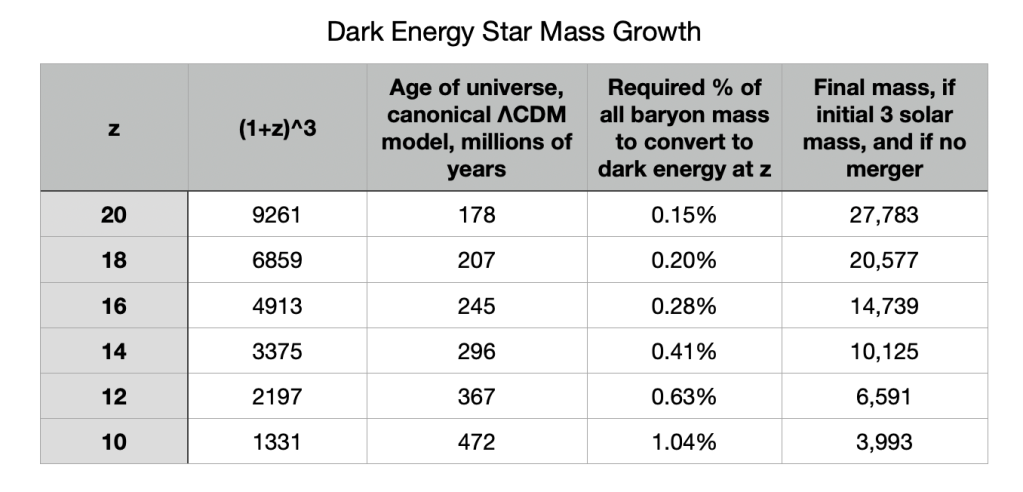
Table 1. The first column has the redshift (epoch) of dark energy star formation. In actuality it will happen over a broad range of redshifts, but the earliest stars and galaxies seem to have formed from around 200 to 500 million years after the Big Bang started. The second column has the mass expansion factor (1+z)3; the DE star’s gravitational mass grows by that factor from the formation z until now. The third column is the age of the universe at DE star formation. The fourth column tells us what fraction of all baryons need to be incorporated into dark energy cores in those stars (they could be somewhat more massive than that). The fifth column is the lower bound on their current mass if they never experience a merger or accretion of other matter. All in all it looks as if less than 1% of baryons convert to dark energy cores.
The fifth column shows the current mass of a minimal 3 solar mass dark energy star at present, noting that 3 solar masses is the lightest known black hole. There may be lighter dark energy stars, but not very much lighter than that, perhaps a little less than 2 solar masses. And the number density should be highest at the low end according to everything we know about star formation.
Now to some degree these are underestimates for the final mass, as shown in the fifth column, since there will be mergers and accretion of other matter into these stars, and of the two effects, the mergers are more important, but they support the general argument. If a dark energy star merges with a neutron star, or other type of black hole, the dark energy core gains in relative terms. So all of this is a plausibility argument that says if the formation is of dark energy stars of a few solar masses in the epoch from 200 to 500 million years after the Big Bang, that less than 1% of all baryons are needed. And it says that the final masses are well into the intermediate range of thousands or tens of thousands of solar masses, and yet they can hide out in galaxies or between galaxies with hundreds of billions of solar masses, only contributing a few percent to the total mass.
Dark energy star cosmology
Dark energy star cosmology needs to agree with the known set of cosmological observations. It has to provide all or a significant fraction of the total dark energy budget in order to be useful. It appears from simple arguments that it can meet the budget by conversion of a small percentage of the baryons in the universe to dark energy stars.
It should exhibit an equation of state w = -1 or nearly so, and it appears to do that. It should not contribute too much mass to upset our galaxy mass estimates. It does that and it does not appear to explain dark matter in any direct way.
Dark energy stars collectively could potentially fill that role. In the model described above it is their collective effects that are being modeled as a dark energy background field that in turn drives dark energy star cores to higher masses over time. Dark energy (as a global field) feeds on itself (the dark energy cores)!
There are some differences with the normal ΛCDM cosmology assumption of a highly uniform dark energy background, not one composed of a very large number of point sources. In particular the ΛCDM cosmology has the dark energy background there from the very beginning, but it is not significant until,the universe has expanded sufficiently.
With the dark energy star case it has to be built up, one dark energy core at a time. So the dark energy effects do not begin until redshifts less than say z = 20 to 30 and most of it may be built up by z = 8 to 10, within the first billion years.
In the dark energy star case we will have accretion of nearby matter including stars, and mergers with neutron stars, other dark energy stars, and other black hole types.
A merger with a neutron star or non dark energy star only increases the mass in dark energy cores; it is positive evolution in the aggregate dark energy core component. A merger of two dark energy stars will lose some of the collective mass in conversion to gravitational radiation, and is a negative contribution toward the overall dark energy budget.
One way to distinguish between the two cosmological models is to push our measurement of the strength of dark energy as far back as we can and look for variations. Another is to identify as many individual intermediate scale black holes / dark energy stars as we can from gravitational wave surveys and from detailed studies of globular clusters and dwarf galaxies.
What about dark matter?
Dark matter’s ratio to ordinary matter at the time of the cosmic microwave background emission is measured to be 5:1 and currently in galaxies and their rotation curves and in clusters of galaxies in their intracluster medium it is also seen to be around 5:1 on average. Since the dark energy cores in the Croker et al. proposal are created hundreds of millions of years after the cosmic microwave background era, then these dark energy stars can not be a major contribution to dark matter per se.
The pair of papers just published by the team doesn’t really discuss dark matter implications. But a previous paper by Croker, Runburg and Farrah (2020) explored the interaction between the dark energy bulk behavior of the global population of dark energy stars with cold dark matter and found little or no affect.
Their process converts a rather small percentage of baryons (or even some dark matter particles) into dark energy and its negative pressure. Such material couples differently to the gravitational field than dark matter, which like ordinary matter is approximately dust-like with an equation of state parameter w = 0.
In the 2020 paper they find that GEODEs or dark energy stars can be spread out even more than dark matter that dominates galaxy halos, or the intracluster medium in rich clusters of galaxies.
Prizes ahead?
This concept of cosmological coupling is one of the most interesting areas of observational and theoretical cosmology in this century. If this work by Croker and collaborators is confirmed the team will be winning prizes in astrophysics and cosmology, since it could be a real breakthrough in both our understanding of the nature of dark energy and our understanding of black hole physics.
In any case, Dark Energy Star already has its own song.
Glossary
Black Hole: A dense collection of matter that collapses inside a small radius, and in theory, to a singularity, and which has sufficiently strong gravity that nothing, not even light, is able to escape. Black holes are characterized by three numbers: mass, angular momentum, and charge.
Cosmological constant: Einstein added this term, Λ, on the left hand side of the equations of general relativity, in a search for a static universe solution. It corresponds to an equation of state parameter w = -1. If the term is moved to the right hand side it becomes a dark energy source term in the stress-energy tensor.
Cosmological coupling: The coupling of local properties to the overall cosmological model. For example, photons redshift to lower energies with the expansion of the universe. It is argued that dark energy stellar cores would collectively couple to the overall Friedmann cosmology that matches the bulk parameters of the universe. In this case it would be a ‘blueshift’ style increase in mass in proportion to the growing volume of the universe, or perhaps more slowly.
Dark Energy: Usually attributed to energy of the vacuum, dark energy has a negative pressure in proportion to its energy density. It was confirmed by Nobel prize winning teams that dark energy is the dominant component of the universe’s mass-energy balance, some 69% of the critical value, and is driving an accelerated expansion with an equation of state w = -1 to within small errors.
Dark Energy Star: A highly compact object that should look like a black hole externally but has no singularity at its core. Instead it has a core of dark energy. If one integrates over all dark energy stars, it may add up to a portion or all of the universe’s dark energy budget. It should have a crust of ‘normal’ matter with anisotropic stress at the boundary with the core, or an intermediate transition zone with varying equation of state between the crust and the core.
Dark Matter: An unknown substance thought to reside in galactic halos, with 5 times as much matter density on average as ordinary matter. Dark matter does not interact electromagnetically and is typically considered to be particulate in nature, although primordial mini black holes have been suggested as one possible explanation.
Equation of state: The relationship between pressure and energy density, P = w * ρ * c^2 where P is pressure and can be negative, and ρ the energy density is positive. If w < -1/3 there is dark pressure, if w = -1 it is the simplest cosmological constant form. Dark matter or a collection of stars or galaxies can be modeled as w ~ 0.
GEODEs: GEneric Objects of Dark Energy, dark energy stars. Formation is thought to occur from Pop III stars, the first stellar generation, at epochs 30 > z > 8.
Gravastar: A stellar model that has a dark energy core and a very thin outer shell. With normal matter added there is anisotropic stress at the boundary to maintain pressure continuity from the core to the shell.
Non-singular black holes: A black hole like object with no singularity.
Primordial black holes: Black holes that may have formed in the very early universe, within the first second. Primordial dark energy stars in large numbers would be problematic, because they would grow in mass by (1 + z)^3 where z >> 1000.
Vacuum energy: The irreducible energy of the vacuum state. The vacuum state is not empty, it is pervaded by fields and virtual particles that pop in and out of existence on very short time scales.
References
https://scitechdaily.com/cosmological-coupling-new-evidence-points-to-black-holes-as-source-of-dark-energy/ – Popular article about the research from University of Hawaii lead authors and collaborators
https://www.phys.hawaii.edu/~kcroker/ – Kevin Croker’s web site at University of Hawaii
Beltracchi, P. and Gondolo, P. 2019, https://arxiv.org/abs/1810.12400 “Formation of Dark Energy Stars”
Croker, K.S. and Weiner J.L. 2019, https://dor.org/10.3847/1538-4357/ab32da “Implications of Symmetry and Pressure in Friedmann Cosmology. I. Formalism”
Croker, K.S., Nishimura, K.A., and Farrah D., 2020 https://arxiv.org/pdf/1904.03781.pdf, “Implications of Symmetry and Pressure in Friedmann Cosmology. II. Stellar Remnant Black Hole Mass Function”
Croker, K.S., Runburg, J., and Farrah D., 2020 https://doi.org/10.3847/1538-4357/abad2f “Implications of Symmetry and Pressure in Friedmann Cosmology. III. Point Sources of Dark Energy that tend toward Uniformity”
Croker, K.S., Zevin, M.J., Farrah, D., Nishimura, K.A., and Tarle, G. 2021, “Cosmologically coupled compact objects: a single parameter model for LIGO-Virgo mass and redshift distributions” https://arxiv.org/pdf/2109.08146.pdf
Farrah, D., Croker, K.S. et al. 2023 February, https://iopscience.iop.org/article/10.3847/2041-8213/acb704/pdf “Observational Evidence for Cosmological Coupling of Black Holes and its Implications for an Astrophysical Source of Dark Energy” (appeared in Ap.J. Letters 20 February, 2023)
Farrah, D., Petty S., Croker K.S. et al. 2023 February, https://doi.org/10.3847/1538-4357/acac2e “A Preferential Growth Channel for Supermassive Black Holes in Elliptical Galaxies at z <~ 2”
Ghezzi, C.R. 2011, https://arxiv.org/pdf/0908.0779.pdf “Anisotropic dark energy stars”
Gliner, E.B. 1965, Algebraic Properties of the Energy-momentum Tensor and Vacuum-like States of Matter. ZhTF 49, 542–548. English transl.: Sov. Phys. JETP 1966, 22, 378.
Harikane, Y., Ouchi, M., et al. arXiv:2208.01612v3, “A Comprehensive Study on Galaxies at z ~ 9 – 16 Found in the Early JWST Data: UV Luminosity Functions and Cosmic Star-Formation History at the Pre-Reionization Epoch”
Perrenod, S.C. 2017, “Dark Energy and the Cosmological Constant” https://darkmatterdarkenergy.com/2017/07/13/dark-energy-and-the-comological-constant/
Whalen, D.J., Even, W. et al.2013, doi:10.1088/004-637X/778/1/17, “Supermassive Population III Supernovae and the Birth of the first Quasars”
Yakovlev, D. and Kaminker, A. 2023, https://arxiv.org/pdf/2301.13150.pdf “Nearly Forgotten Cosmological Concept of E.B. Gliner”