Is gravity fundamental or emergent? Electromagnetism is one example of a fundamental force. Thermodynamics is an example of emergent, statistical behavior.
Newton saw gravity as a mysterious force acting at a distance between two objects, obeying the well-known inverse square law, and occurring in a spacetime that was inflexible, and had a single frame of reference.
Einstein looked into the nature of space and time and realized they are flexible. Yet general relativity is still a classical theory, without quantum behavior. And it presupposes a continuous fabric for space.
As John Wheeler said, “spacetime tells matter how to move; matter tells spacetime how to curve”. Now Wheeler full well knew that not just matter, but also energy, curves spacetime.
A modest suggestion: invert Wheeler’s sentence. And then generalize it. Matter, and energy, tells spacetime how to be.
Which is more fundamental? Matter or spacetime?
Quantum theories of gravity seek to couple the known quantum fields with gravity, and it is expected that at the extremely small Planck scales, time and space both lose their continuous nature.
In physics, space and time are typically assumed as continuous backdrops.
But what if space is not fundamental at all? What if time is not fundamental? It is not difficult to conceive of time as merely an ordering of events. But space and time are to some extent interchangeable, as Einstein showed with special relativity.
So what about space? Is it just us placing rulers between objects, between masses?
Particle physicists are increasingly coming to the view that space, and time, are emergent. Not fundamental.
If emergent, from what? The concept is that particles, and quantum fields, for that matter, are entangled with one another. Their microscopic quantum states are correlated. The phenomenon of quantum entanglement has been studied in the laboratory and is well proven.
Chinese scientists have even, just last year, demonstrated quantum entanglement of photons over a satellite uplink with a total path exceeding 1200 kilometers.
Quantum entanglement thus becomes the thread Nature uses to stitch together the fabric of space. And as the degree of quantum entanglement changes the local curvature of the fabric changes. As the curvature changes, matter follows different paths. And that is gravity in action.
Newton’s laws are an approximation of general relativity for the case of small accelerations. But if space is not a continuous fabric and results from quantum entanglement, then for very small accelerations (in a sub-Newtonian range) both Newton dynamics and general relativity may be incomplete.
The connection between gravity and thermodynamics has been around for four decades, through research on black holes, and from string theory. Jacob Bekenstein and Stephen Hawking determined that a black hole possesses entropy proportional to its area divided by the gravitational constant G. This area law entropy approach can be used to derive general relativity as Ted Jacobson did in 1995.
But it may be that the supposed area law component is insufficient; according to Erik Verlinde’s new emergent gravity hypothesis, there is also a volume law component for entropy, that must be considered due to dark energy and when accelerations are very low.
We have had hints about this incomplete description of gravity in the velocity measurements made at the outskirts of galaxies during the past eight decades. Higher velocities than expected are seen, reflecting higher acceleration of stars and gas than Newton (or Einstein) would predict. We can call this dark gravity.
Now this dark gravity could be due to dark matter. Or it could just be modified gravity, with extra gravity over what we expected.
It has been understood since the work of Mordehai Milgrom in the 1980s that the excess velocities that are observed are better correlated with extra acceleration than with distance from the galactic center.
Stacey McGaugh and collaborators have demonstrated a very tight correlation between the observed accelerations and the expected Newtonian acceleration, as I discussed in a prior blog here. The extra acceleration kicks in below a few times  meters per second per second (m/s²).
meters per second per second (m/s²).
This is suspiciously close to the speed of light divided by the age of the universe! Which is about  m/s².
m/s².
Why should that be? The mass/energy density (both mass and energy contribute to gravity) of the universe is dominated today by dark energy.
The canonical cosmological model has 70% dark energy, 25% dark matter, and 5% ordinary matter. In fact if there is no dark matter, just dark gravity, or dark acceleration, then it could be more like a 95% and 5% split between dark energy and (ordinary) matter components.
A homogeneous universe composed only of dark energy in general relativity is known as a de Sitter (dS) universe. Our universe is, at present, basically a dS universe ‘salted’ with matter.
Then one needs to ask how does gravity behave in dark energy influenced domains? Now unlike ordinary matter, dark energy is highly uniformly distributed on the largest scales. It is driving an accelerated expansion of the universe (the fabric of spacetime!) and dragging the ordinary matter along with it.
But where the density of ordinary matter is high, dark energy is evacuated. An ironic thought, since dark energy is considered to be vacuum energy. But where there is lots of matter, the vacuum is pushed aside.
That general concept was what Erik Verlinde used to derive an extra acceleration formula in 2016. He modeled an emergent, entropic gravity due to ordinary matter and also due to the interplay between dark energy and ordinary matter. He modeled the dark energy as responding like an elastic medium when it is displaced within the vicinity of matter. Using this analogy with elasticity, he derived an extra acceleration as proportional to the square root of the product of the usual Newtonian acceleration and a term related to the speed of light divided by the universe’s age. This leads to a 1/r force law for the extra component since Newtonian acceleration goes as 1/r².
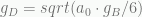
Verlinde’s dark gravity depends on the square root of the product of a characteristic acceleration a0 and ordinary Newtonian (baryonic) gravity, gB
The idea is that the elastic, dark energy medium, relaxes over a cosmological timescales. Matter displaces energy and entropy from this medium, and there is a back reaction of the dark energy on matter that is expressed as a volume law entropy. Verlinde is able to show that this interplay between the matter and dark energy leads precisely to the characteristic acceleration is  , where H is the Hubble expansion parameter and is equal to one over the age of the universe for a dS universe. This turns out be the right value of just over
, where H is the Hubble expansion parameter and is equal to one over the age of the universe for a dS universe. This turns out be the right value of just over  m/s² that matches observations.
m/s² that matches observations.
In our solar system, and indeed in the central regions of galaxies, we see gravity as the interplay of ordinary matter and other ordinary matter. We are not used to this other dance.
Domains of gravity
|
Acceleration
|
Domain |
Gravity vis-a-vis Newtonian formula |
Examples
|
| High (GM/R ~ c²) |
Einstein, general relativity |
Higher |
Black holes, neutron stars
|
| Normal |
Newtonian dynamics |
1/r² |
Solar system, Sun orbit in Milky Way |
|
Very low (< c/ age of U.)
|
Dark Gravity |
Higher, additional 1/r term |
Outer edges of galaxies, dwarf galaxies, clusters of galaxies |
The table above summarizes three domains for gravity: general relativity, Newtonian, and dark gravity, the latter arising at very low accelerations. We are always calculating gravity incorrectly! Usually, such as in our solar system, it matters not at all. For example at the Earth’s surface gravity is 11 orders of magnitude greater than the very low acceleration domain where the extra term kicks in.
Recently, Alexander Peach, a Teaching Fellow in physics at Durham University, has taken a different angle based on Verlinde’s original, and much simpler, exposition of his emergent gravity theory in his 2010 paper. He derives an equivalent result to Verlinde’s in a way which I believe is easier to understand. He assumes that holography (the assumption that all of the entropy can be calculated as area law entropy on a spherical screen surrounding the mass) breaks down at a certain length scale. To mimic the effect of dark energy in Verlinde’s new hypothesis, Peach adds a volume law contribution to entropy which competes with the holographic area law at this certain length scale. And he ends up with the same result, an extra 1/r entropic force that should be added for correctness in very low acceleration domains.

In figure 2 (above) from Peach’s paper he discusses a test particle located beyond a critical radius  for which volume law entropy must also be considered. Well within
for which volume law entropy must also be considered. Well within  (shown in b) the dark energy is fully displaced by the attracting mass located at the origin and the area law entropy calculation is accurate (indicated by the shaded surface). Beyond
(shown in b) the dark energy is fully displaced by the attracting mass located at the origin and the area law entropy calculation is accurate (indicated by the shaded surface). Beyond  the dark energy effect is important, the holographic screen approximation breaks down, and the volume entropy must be included in the contribution to the emergent gravitational force (shown in c). It is this volume entropy that provides an additional 1/r term for the gravitational force.
the dark energy effect is important, the holographic screen approximation breaks down, and the volume entropy must be included in the contribution to the emergent gravitational force (shown in c). It is this volume entropy that provides an additional 1/r term for the gravitational force.
Peach makes the assumption that the bulk and boundary systems are in thermal equilibrium. The bulk is the source of volume entropy. In his thought experiment he models a single bit of information corresponding to the test particle being one Compton wavelength away from the screen, just as Verlinde initially did in his description of emergent Newtonian gravity in 2010. The Compton wavelength is equal to the wavelength a photon would have if its energy were equal to the rest mass energy of the test particle. It quantifies the limitation in measuring the position of a particle.
Then the change in boundary (screen) entropy can be related to the small displacement of the particle. Assuming thermal equilibrium and equipartition within each system and adopting the first law of thermodynamics, the extra entropic force can be determined as equal to the Newtonian formula, but replacing one of the r terms in the denominator by  .
.
To understand  , for a given system, it is the radius at which the extra gravity is equal to the Newtonian calculation, in other words, gravity is just twice as strong as would be expected at that location. In turn, this traces back to the fact that, by definition, it is the length scale beyond which the volume law term overwhelms the holographic area law.
, for a given system, it is the radius at which the extra gravity is equal to the Newtonian calculation, in other words, gravity is just twice as strong as would be expected at that location. In turn, this traces back to the fact that, by definition, it is the length scale beyond which the volume law term overwhelms the holographic area law.
It is thus the distance at which the Newtonian gravity alone drops to about 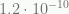 m/s², i.e.
m/s², i.e.  , for a given system.
, for a given system.
So Peach and Verlinde use two different methods but with consistent assumptions to model a dark gravity term which follows a 1/r force law. And this kicks in at around  m/s².
m/s².
The ingredients introduced by Peach’s setup may be sufficient to derive a covariant theory, which would entail a modified version of general relativity that introduces new fields, which could have novel interactions with ordinary matter. This could add more detail to the story of covariant emergent gravity already considered by Hossenfelder (2017), and allow for further phenomenological testing of emergent dark gravity. Currently, it is not clear what the extra degrees of freedom in the covariant version of Peach’s model should look like. It may be that Verlinde’s introduction of elastic variables is the only sensible option, or it could be one of several consistent choices.
With Peach’s work, physicists have taken another step in understanding and modeling dark gravity in a fashion that obviates the need for dark matter to explain our universe
We close with another of John Wheeler’s sayings:
“The only thing harder to understand than a law of statistical origin would be a law that is not of statistical origin, for then there would be no way for it—or its progenitor principles—to come into being. On the other hand, when we view each of the laws of physics—and no laws are more magnificent in scope or better tested—as at bottom statistical in character, then we are at last able to forego the idea of a law that endures from everlasting to everlasting. “
It is a pleasure to thank Alexander Peach for his comments on, and contributions to, this article.
References:
https://darkmatterdarkenergy.com/2018/08/02/dark-acceleration-the-acceleration-discrepancy/ blog “Dark Acceleration: The Acceleration Discrepancy”
https://arxiv.org/abs/gr-qc/9504004 “Thermodynamics of Spacetime: The Einstein Equation of State” 1995, Ted Jacobson
https://darkmatterdarkenergy.com/2017/07/13/dark-energy-and-the-comological-constant/ blog “Dark Energy and the Cosmological Constant”
https://darkmatterdarkenergy.com/2016/12/30/emergent-gravity-verlindes-proposal/ blog “Emergent Gravity: Verlinde’s Proposal”
https://arxiv.org/pdf/1806.10195.pdf “Emergent Dark Gravity from (Non) Holographic Screens” 2018, Alexander Peach
https://arxiv.org/pdf/1703.01415.pdf “A Covariant Version of Verlinde’s Emergent Gravity” Sabine Hossenfelder














