Tag Archives: Erik Verlinde

March 12, 2017

Emergent Gravity in the Solar System

In a prior post I outlined Erik Verlinde’s recent proposal for Emergent Gravity that may obviate the need for dark matter.

Emergent gravity is a statistical, thermodynamic phenomenon that emerges from the underlying quantum entanglement of micro states found in dark energy and in ordinary matter. Most of the entropy is in the dark energy, but the presence of ordinary baryonic matter can displace entropy in its neighborhood and the dark energy exerts a restoring force that is an additional contribution to gravity.

Emergent gravity yields both an area entropy term that reproduces general relativity (and Newtonian dynamics) and a volume entropy term that provides extra gravity. The interesting point is that this is coupled to the cosmological parameters, basically the dark energy term which now dominates our de Sitter-like universe and which acts like a cosmological constant Λ.

In a paper that appeared in arxiv.org last month, a trio of astronomers Hees, Famaey and Bertone claim that emergent gravity fails by seven orders of magnitude in the solar system. They look at the advance of the perihelion for six planets out through Saturn and claim that Verlinde’s formula predicts perihelion advances seven orders of magnitude larger than should be seen.

hst_saturn_nicmos

No emergent gravity needed here. Image credit: NASA GSFC

But his formula does not apply in the solar system.

“..the authors claiming that they have ruled out the model by seven orders of magnitude using solar system data. But they seem not to have taken into account that the equation they are using does not apply on solar system scales. Their conclusion, therefore, is invalid.” – Sabine Hossenfelder, theoretical physicist (quantum gravity) Forbes blog

Why is this the case? Verlinde makes 3 main assumptions: (1) a spherically symmetric, isolated system, (2) a system that is quasi-static, and (3) a de Sitter spacetime. Well, check for (1) and check for (2) in the case of the Solar System. However, the Solar System is manifestly not a dark energy-dominated de Sitter space.

It is overwhelmingly dominated by ordinary matter. In our Milky Way galaxy the average density of ordinary matter is some 45,000 times larger than the dark energy density (which corresponds to only about 4 protons per cubic meter). And in our Solar System it is concentrated in the Sun, but on average out to the orbit of Saturn is a whopping $3.7 \cdot 10^{17}$ times the dark energy density.

The whole derivation of the Verlinde formula comes from looking at the incremental entropy (contained in the dark energy) that is displaced by ordinary matter. Well with over 17 orders of magnitude more energy density, one can be assured that all of the dark energy entropy was long ago displaced within the Solar System, and one is well outside of the domain of Verlinde’s formula, which only becomes relevant when acceleration drops near to or below c * H. The Verlinde acceleration parameter takes the value of $1.1 \cdot 10^{-8}$ centimeters/second/second for the observed value of the Hubble parameter. The Newtonian acceleration at Saturn is .006 centimeters/second/second or 50,000 times larger.

The conditions where dark energy is being displaced only occur when the gravity has dropped to much smaller values; his approximation is not simply a second order term that can be applied in a domain where dark energy is of no consequence.

There is no entropy left to displace, and thus the Verlinde formula is irrelevant at the orbit of Saturn, or at the orbit of Pluto, for that matter. The authors have not disproven Verlinde’s proposal for emergent gravity.

5 Comments | tags: Dark energy, Dark matter, emergent gravity, Erik Verlinde, Saturn, solar system | posted in Dark Energy, Dark Matter

December 30, 2016

Emergent Gravity: Verlinde’s Proposal

By darkmatterdarkenergy

In a previous blog entry I give some background around Erik Verlinde’s proposal for an emergent, thermodynamic basis of gravity. Gravity remains mysterious 100 years after Einstein’s introduction of general relativity – because it is so weak relative to the other main forces, and because there is no quantum mechanical description within general relativity, which is a classical theory.

One reason that it may be so weak is because it is not fundamental at all, that it represents a statistical, emergent phenomenon. There has been increasing research into the idea of emergent spacetime and emergent gravity and the most interesting proposal was recently introduced by Erik Verlinde at the University of Amsterdam in a paper “Emergent Gravity and the Dark Universe”.

A lot of work has been done assuming anti-de Sitter (AdS) spaces with negative cosmological constant Λ – just because it is easier to work under that assumption. This year, Verlinde extended this work from the unrealistic AdS model of the universe to a more realistic de Sitter (dS) model. Our runaway universe is approaching a dark energy dominated dS solution with a positive cosmological constant Λ.

The background assumption is that quantum entanglement dictates the structure of spacetime, and its entropy and information content. Quantum states of entangled particles are coherent, observing a property of one, say the spin orientation, tells you about the other particle’s attributes; this has been observed in long distance experiments, with separations exceeding 100 kilometers.

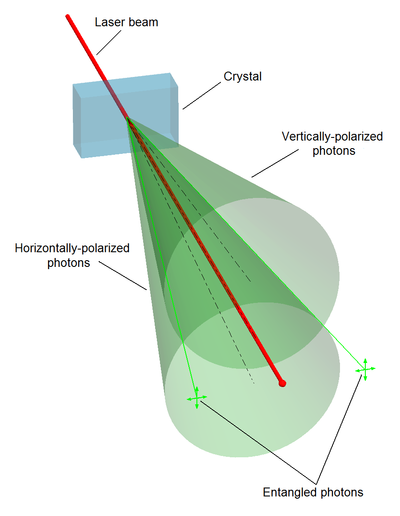If space is defined by the connectivity of quantum entangled particles, then it becomes almost natural to consider gravity as an emergent statistical attribute of the spacetime. After all, we learned from general relativity that “matter tells space how to curve, curved space tells matter how to move” – John Wheeler.

What if entanglement tells space how to curve, and curved space tells matter how to move? What if gravity is due to the entropy of the entanglement? Actually, in Verlinde’s proposal, the entanglement entropy from particles is minor, it’s the entanglement of the vacuum state, of dark energy, that dominates, and by a very large factor.

One analogy is thermodynamics, which allows us to represent the bulk properties of the atmosphere that is nothing but a collection of a very large number of molecules and their micro-states. Verlinde posits that the information and entropy content of space are due to the excitations of the vacuum state, which is manifest as dark energy.

The connection between gravity and thermodynamics has been around for 3 decades, through research on black holes, and from string theory. Jacob Bekenstein and Stephen Hawking determined that a black hole possesses entropy proportional to its area divided by the gravitational constant G. String theory can derive the same formula for quantum entanglement in a vacuum. This is known as the AdS/CFT (conformal field theory) correspondence.

So in the AdS model, gravity is emergent and its strength, the acceleration at a surface, is determined by the mass density on that surface surrounding matter with mass M. This is just the inverse square law of Newton. In the more realistic dS model, the entropy in the volume, or bulk, must also be considered. (This is the Gibbs entropy relevant to excited states, not the Boltzmann entropy of a ground state configuration).

Newtonian dynamics and general relativity can be derived from the surface entropy alone, but do not reflect the volume contribution. The volume contribution adds an additional term to the equations, strengthening gravity over what is expected, and as a result, the existence of dark matter is ‘spoofed’. But there is no dark matter in this view, just stronger gravity than expected.

This is what the proponents of MOND have been saying all along. Mordehai Milgrom observed that galactic rotation curves go flat at a characteristic low acceleration scale of order 2 centimeters per second per year. MOND is phenomenological, it observes a trend in galaxy rotation curves, but it does not have a theoretical foundation.

Verlinde’s proposal is not MOND, but it provides a theoretical basis for behavior along the lines of what MOND states.

Now the volume in question turns out to be of order the Hubble volume, which is defined as c/H, where H is the Hubble parameter denoting the rate at which galaxies expand away from one another. Reminder: Hubble’s law is $v = H \cdot d$ where v is the recession velocity and the d the distance between two galaxies. The lifetime of the universe is approximately 1/H.

clusters_1280.abell1835.jpg

The value of c / H is over 4 billion parsecs (one parsec is 3.26 light-years) so it is in galaxies, clusters of galaxies, and at the largest scales in the universe for which departures from general relativity (GR) would be expected.

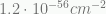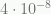Dark energy in the universe takes the form of a cosmological constant Λ, whose value is measured to be $1.2 \cdot 10^{-56} cm^{-2}$ . Hubble’s parameter is $2.2 \cdot 10^{-18} sec^{-1}$ . A characteristic acceleration is thus H²/ sqrt(Λ) or $4 \cdot 10^{-8}$ cm per sec per sec (cm = centimeters, sec = second).

One can also define a cosmological acceleration scale simply by 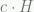$c \cdot H$ , the value for this is about $6 \cdot 10^{-8}$ cm per sec per sec (around 2 cm per sec per year), and is about 15 billion times weaker than Earth’s gravity at its surface! Note that the two estimates are quite similar.

This is no coincidence since we live in an approximately dS universe, with a measured Λ ~ 0.7 when cast in terms of the critical density for the universe, assuming the canonical ΛCDM cosmology. That’s if there is actually dark matter responsible for 1/4 of the universe’s mass-energy density. Otherwise Λ could be close to 0.95 times the critical density. In a fully dS universe, $\Lambda \cdot c^2 = 3 \cdot H^2$ , so the two estimates should be equal to within $sqrt(3)$ which is approximately the difference in the two estimates.

So from a string theoretic point of view, excitations of the dark energy field are fundamental. Matter particles are bound states of these excitations, particles move freely and have much lower entropy. Matter creation removes both energy and entropy from the dark energy medium. General relativity describes the response of area law entanglement of the vacuum to matter (but does not take into account volume entanglement).

Verlinde proposes that dark energy (Λ) and the accelerated expansion of the universe are due to the slow rate at which the emergent spacetime thermalizes. The time scale for the dynamics is 1/H and a distance scale of c/H is natural; we are measuring the time scale for thermalization when we measure H. High degeneracy and slow equilibration means the universe is not in a ground state, thus there should be a volume contribution to entropy.

When the surface mass density falls below 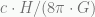$c \cdot H / (8 \pi \cdot G)$ things change and Verlinde states the spacetime medium becomes elastic. The effective additional ‘dark’ gravity is proportional to the square root of the ordinary matter (baryon) density and also to the square root of the characteristic acceleration $c \cdot H$ .

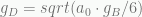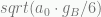This dark gravity additional acceleration satisfies the equation $g _D = sqrt {(a_0 \cdot g_B / 6 )}$ , where $g_B$ is the usual Newtonian acceleration due to baryons and $a_0 = c \cdot H$ is the dark gravity characteristic acceleration. The total gravity is $g = g_B + g_D$ . For large accelerations this reduces to the usual $g_B$ and for very low accelerations it reduces to $sqrt {(a_0 \cdot g_B / 6 )}$ .

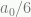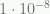The value $a_0/6$ at $1 \cdot 10^{-8}$ cm per sec per sec derived from first principles by Verlinde is quite close to the MOND value of Milgrom, determined from galactic rotation curve observations, of 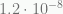$1.2 \cdot 10^{-8}$ cm per sec per sec.

So suppose we are in a region where 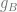$g_B$ is only 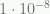$1 \cdot 10^{-8}$ cm per sec per sec. Then 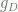$g_D$ takes the same value and the gravity is just double what is expected. Since orbital velocities go as the square of the acceleration then the orbital velocity is observed to be $sqrt(2)$ higher than expected.

In terms of gravitational potential, the usual Newtonian potential goes as 1/r, resulting in a 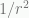$1/r^2$ force law, whereas for very low accelerations the potential now goes as 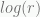$log(r)$ and the resultant force law is 1/r. We emphasize that while the appearance of dark matter is spoofed, there is no dark matter in this scenario, the reality is additional dark gravity due to the volume contribution to the entropy (that is displaced by ordinary baryonic matter).

Flat to rising rotation curve for the galaxy M33

Dark matter was first proposed by Swiss astronomer Fritz Zwicky when he observed the Coma Cluster and the high velocity dispersions of the constituent galaxies. He suggested the term dark matter (“dunkle materie”). Harold Babcock in 1937 measured the rotation curve for the Andromeda galaxy and it turned out to be flat, also suggestive of dark matter (or dark gravity). Decades later, in the 1970s and 1980s, Vera Rubin (just recently passed away) and others mapped many rotation curves for galaxies and saw the same behavior. She herself preferred the idea of a deviation from general relativity over an explanation based on exotic dark matter particles. One needs about 5 times more matter, or about 5 times more gravity to explain these curves.

Verlinde is also able to derive the Tully-Fisher relation by modeling the entropy displacement of a dS space. The Tully-Fisher relation is the strong observed correlation between galaxy luminosity and angular velocity (or emission line width) for spiral galaxies, 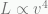$L \propto v^4$ . With Newtonian gravity one would expect $M \propto v^2$ . And since luminosity is essentially proportional to ordinary matter in a galaxy, there is a clear deviation by a ratio of v².

Apparent distribution of spoofed dark matter, for a given ordinary (baryonic) matter distribution

When one moves to the scale of clusters of galaxies, MOND is only partially successful, explaining a portion, coming up shy a factor of 2, but not explaining all of the apparent mass discrepancy. Verlinde’s emergent gravity does better. By modeling a general mass distribution he can gain a factor of 2 to 3 relative to MOND and basically it appears that he can explain the velocity distribution of galaxies in rich clusters without the need to resort to any dark matter whatsoever.

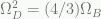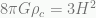And, impressively, he is able to calculate what the apparent dark matter ratio should be in the universe as a whole. The value is $\Omega_D^2 = (4/3) \Omega_B$ where $\Omega_D$ is the apparent mass-energy fraction in dark matter and $\Omega_B$ is the actual baryon mass density fraction. Both are expressed normalized to the critical density determined from the square of the Hubble parameter, $8 \pi G \rho_c = 3 H^2$ .

Plugging in the observed $\Omega_B \approx 0.05$ one obtains $\Omega_D \approx 0.26$ , very close to the observed value from the cosmic microwave background observations. The Planck satellite results have the proportions for dark energy, dark matter, ordinary matter as .68, .27, and .05 respectively, assuming the canonical ΛCDM cosmology.

The main approximations Verlinde makes are a fully dS universe and an isolated, static (bound) system with a spherical geometry. He also does not address the issue of galaxy formation from the primordial density perturbations. At first guess, the fact that he can get the right universal $\Omega_D$ suggests this may not be a great problem, but it requires study in detail.

Breaking News!

Margot Brouwer and co-researchers have just published a test of Verlinde’s emergent gravity with gravitational lensing. Using a sample of over 33,000 galaxies they find that general relativity and emergent gravity can provide an equally statistically good description of the observed weak gravitational lensing. However, emergent gravity does it with essentially no free parameters and thus is a more economical model.

“The observed phenomena that are currently attributed to dark matter are the consequence of the emergent nature of gravity and are caused by an elastic response due to the volume law contribution to the entanglement entropy in our universe.” – Erik Verlinde

References

Erik Verlinde 2011 “On the Origin of Gravity and the Laws of Newton” arXiv:1001.0785

Stephen Perrenod, 2013, 2nd edition, “Dark Matter, Dark Energy, Dark Gravity” Amazon, provides the traditional view with ΛCDM (read Dark Matter chapter with skepticism!)

Erik Verlinde 2016 “Emergent Gravity and the Dark Universe arXiv:1611.02269v1

Margot Brouwer et al. 2016 “First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing Measurements” arXiv:1612.03034v

9 Comments | tags: black hole entropy, clusters of galaxies, Dark energy, Dark matter, emergent gravity, entropic gravity, Erik Verlinde, fritz zwicky, galaxy rotation curves, general relativity, gravitational lensing, margot brouwer, modified gravity, modified newtonian dynamics, MOND, thermodynamic gravity, vera rubin | posted in Dark Energy, Dark Matter, Gravity

November 26, 2016

Dark Gravity: Is Gravity Thermodynamic?

By darkmatterdarkenergy

This is the first in a series of articles on ‘dark gravity’ that look at emergent gravity and modifications to general relativity. In my book Dark Matter, Dark Energy, Dark Gravity I explained that I had picked Dark Gravity to be part of the title because of the serious limitations in our understanding of gravity. It is not like the other 3 forces; we have no well accepted quantum description of gravity. And it is some 33 orders of magnitude weaker than those other forces.
I noted that:

The big question here is ~ why is gravity so relatively weak, as compared to the other 3 forces of nature? These 3 forces are the electromagnetic force, the strong nuclear force, and the weak nuclear force. Gravity is different ~ it has a dark or hidden side. It may very well operate in extra dimensions… http://amzn.to/2gKwErb

My major regret with the book is that I was not aware of, and did not include a summary of, Erik Verlinde’s work on emergent gravity. In emergent gravity, gravity is not one of the fundamental forces at all.

Erik Verlinde is a leading string theorist in the Netherlands who in 2009 proposed that gravity is an emergent phenomenon, resulting from the thermodynamic entropy of the microstates of quantum fields.

In 2009, Verlinde showed that the laws of gravity may be derived by assuming a form of the holographic principle and the laws of thermodynamics. This may imply that gravity is not a true fundamental force of nature (like e.g. electromagnetism), but instead is a consequence of the universe striving to maximize entropy. – Wikipedia article “Erik Verlinde”

This year, Verlinde extended this work from an unrealistic anti-de Sitter model of the universe to a more realistic de Sitter model. Our runaway universe is approaching a dark energy dominated deSitter solution.

He proposes that general relativity is modified at large scales in a way that mimics the phenomena that have generally been attributed to dark matter. This is in line with MOND, or Modified Newtonian Dynamics. MOND is a long standing proposal from Mordehai Milgrom, who argues that there is no dark matter, rather that gravity is stronger at large distances than predicted by general relativity and Newton’s laws.

In a recent article on cosmology and the nature of gravity Dr.Thanu Padmanabhan lays out 6 issues with the canonical Lambda-CDM cosmology based on general relativity and a homogeneous, isotropic, expanding universe. Observations are highly supportive of such a canonical model, with a very early inflation phase and with 1/3 of the mass-energy content in dark energy and 2/3 in matter, mostly dark matter.

And yet,

1. The equation of state (pressure vs. density) of the early universe is indeterminate in principle, as well as in practice.

2. The history of the universe can be modeled based on just 3 energy density parameters: i) density during inflation, ii) density at radiation – matter equilibrium, and iii) dark energy density at late epochs. Both the first and last are dark energy driven inflationary de Sitter solutions, apparently unconnected, and one very rapid, and one very long lived. (No mention of dark matter density here).

3. One can construct a formula for the information content at the cosmic horizon from these 3 densities, and the value works out to be 4π to high accuracy.

4. There is an absolute reference frame, for which the cosmic microwave background is isotropic. There is an absolute reference scale for time, given by the temperature of the cosmic microwave background.

5. There is an arrow of time, indicated by the expansion of the universe and by the cooling of the cosmic microwave background.

6. The universe has, rather uniquely for physical systems, made a transition from quantum behavior to classical behavior.

“The evolution of spacetime itself can be described in a purely thermodynamic language in terms of suitably defined degrees of freedom in the bulk and boundary of a 3-volume.”

Now in fluid mechanics one observes:

“First, if we probe the fluid at scales comparable to the mean free path, you need to take into account the discreteness of molecules etc., and the fluid description breaks down. Second, a fluid simply might not have reached local thermodynamic equilibrium at the scales (which can be large compared to the mean free path) we are interested in.”

Now it is well known that general relativity as a classical theory must break down at very small scales (very high energies). But also with such a thermodynamic view of spacetime and gravity, one must consider the possibility that the universe has not reached a statistical equilibrium at the largest scales.

One could have reached equilibrium at macroscopic scales much less than the Hubble distance scale c/H (14 billion light-years, H is the Hubble parameter) but not yet reached it at the Hubble scale. In such a case the standard equations of gravity (general relativity) would apply only for the equilibrium region and for accelerations greater than the characteristic Hubble acceleration scale of $c \cdot H$ (2 centimeters per second / year).

This lack of statistical equilibrium implies the universe could behave similarly to non-equilibrium thermodynamics behavior observed in the laboratory.

The information content of the expanding universe reflects that of the quantum state before inflation, and this result is 4π in natural units by information theoretic arguments similar to those used to derive the entropy of a black hole.

The black hole entropy is $S = A / (4 \cdot Lp^2)$ where A is the area of the black hole using the Schwarzschild radius formula and Lp is the Planck length, $G \hbar / c^3$ , where G is the gravitational constant, $\hbar$ is Planck’s constant.

This beautiful Bekenstein-Hawking entropy formula connects thermodynamics, the quantum world and gravity.

This same value of the universe’s entropy can also be used to determine the number of e-foldings during inflation to be 6 π² or 59, consistent with the minimum value to enforce a sufficiently homogeneous universe at the epoch of the cosmic microwave background.

If inflation occurs at a reasonable ~ $10^{15}$ GeV, one can derive the observed value of the cosmological constant (dark energy) from the information content value as well, argues Dr. Padmanhaban.

This provides a connection between the two dark energy driven de Sitter phases, inflation and the present day runaway universe.

The table below summarizes the 4 major phases of the universe’s history, including the matter dominated phase, which may or may not have included dark matter. Erik Verlinde in his new work, and Milgrom for over 3 decades, question the need for dark matter.

Epoch / Dominated / Ends at / a-t scaling / Size at end

Inflation / Inflaton (dark energy) / $10^{-32}$ seconds / $e^{Ht}$ (de Sitter) / 10 cm

Radiation / Radiation / 40,000 years / $\sqrt t$ / 10 million light-years

Matter / Matter (baryons) Dark matter? / 9 billion light-years / $t^{2/3}$ / > 100 billion light-years

Runaway / Dark energy (Cosmological constant) / “Infinity” / $e^{Ht}$ (de Sitter) / “Infinite”

In the next article I will review the status of MOND – Modified Newtonian Dynamics, from the phenomenology and observational evidence.

References

E. Verlinde. “On the Origin of Gravity and the Laws of Newton”. JHEP. 2011 (04): 29 http://arXiv.org/abs/1001.0785

T. Padmanabhan, 2016. “Do We Really Understand the Cosmos?” http://arxiv.org/abs/1611.03505v1

S. Perrenod, 2011. https://darkmatterdarkenergy.com/2011/07/04/dark-energy-drives-a-runaway-universe/

S. Perrenod, 2011. Dark Matter, Dark Energy, Dark Gravity 2011 http://amzn.to/2gKwErb

S. Carroll and G. Remmen, 2016, http://www.preposterousuniverse.com/blog/2016/02/08/guest-post-grant-remmen-on-entropic-gravity/

2 Comments | tags: Dark energy, dark gravity, Dark matter, emergent gravity, Erik Verlinde, modified gravity, modified newtonian dynamics, MOND, thermodynamics | posted in Big Bang & Inflation, Dark Energy, Dark Matter

Dark Matter, Dark Energy, Dark Gravity

Tag Archives: Erik Verlinde

Emergent Gravity in the Solar System

Emergent Gravity: Verlinde’s Proposal

Dark Gravity: Is Gravity Thermodynamic?

Blog Stats

Lost in Translation

Archives