Tag Archives: general relativity

April 3, 2019

Modified Gravity

By darkmatterdarkenergy

We don’t Need no Stinkin’ Dark Matter

Extra Acceleration

You’ve heard of dark matter, right? Some sort of exotic particle that lurks in the outskirts of galaxies.

Maybe you know the story of elusive dark matter. The first apparent home for dark matter was in clusters of galaxies, as Fritz Zwicky postulated for the Coma Cluster in the 1930s, due to the excessive galaxy random motions that he measured.

There have been eight decades of discovery and measurement of the gravitational anomalies that dark matter is said to cause, and eight decades of notable failure to directly find any very faint ordinary matter, black holes, or exotic particle matter in sufficient quantities to explain the magnitude of the observed anomalies.

If dark matter is actually real and composed of particles or primordial black holes then there is five times as much mass per unit volume on average in that form as there is in the form of ordinary matter. Ordinary matter is principally in the form of protons and neutrons, primarily as hydrogen and helium atoms and ions. 

Why do we call it dark? It gives off no light. Ordinary matter gives off light, it radiates. What else gives off no light? A gravitational field stronger than predicted by existing laws.

Gravitational anomalies are seen in the outer regions of galaxies by examining galaxy rotation curves, which flatten out unexpectedly with distance from the galactic center.  They are seen in galaxy groups and clusters from measuring galaxy velocity dispersions, from X-ray observations of intracluster gas, and from gravitational lensing measurements. A dark matter component is also deduced at the cosmic scale from the power spectrum of the cosmic microwave background spatial variations.

The excessive velocities due to extra acceleration are either caused by dark matter or by some departure of gravity over and above the predictions of general relativity. 

Actually at high accelerations general relativity is the required model but at low accelerations Newtonian dynamics is an accurate approximation. The discrepancies arise only at very low accelerations. These excess velocities, X-ray emission, and lensing are observed only at very low accelerations, so we are basically talking about an alternative of extra gravity which is over and above the 1/r² law for Newtonian dynamics.

Alternatives to General Relativity and Newtonian Dynamics

There are multiple proposed laws for modifying gravity at very low accelerations. To match observations the effect should start to kick in for accelerations less than c * H, where H is the Hubble expansion parameter and its inverse is nearly equal to the present age of the universe. 

That is only around 1 part in 14 million expressed in units of centimeters per second per second. This is not something typically measurable in Earth-bound laboratories; scientists have trouble pinning down the value of the gravitational constant G to within 1 part in 10,000. 

This is a rather profound coincidence, suggesting that there is something fundamental at play in the nature of gravity itself, not necessarily a rather arbitrary creation of exotic dark matter particle in the very early universe. It suggests instead that there is an additional component of gravity tied in some way to the age and state of our universe.

Do you think of general relativity as the last word on gravity? From an Occam’s razor point of view it is actually simpler to think about modifying the laws of gravity in very low acceleration environments, than to postulate an exotic never-seen-in-the-lab dark matter particle. And we already know that general relativity is incomplete, since it is not a quantum theory.

The emergent gravity concept neatly solves the quantum issue by saying gravity is not fundamental in the way that electromagnetism and the nuclear forces are. Rather it is described as an emergent property of a system due to quantum entanglement of fields and particles. In this view, the fabric of space also arises from this entanglement. Gravity is a statistical property of the system, the entropy (in thermodynamic terms) of entanglement at each point.

Dark Energy

Now we have a necessary aside on dark energy. Do you know that dark energy is on firmer standing now than dark matter? And do you know that dark energy is just described by additional energy and pressure components in the stress-energy tensor, fully described within general relativity?

We know that dark energy dominates over dark matter in the canonical cosmological model (Lambda-Cold Dark Matter) for the universe. The canonical model has about 2/3 dark energy and the solution for the universe’s expansion approximates a de Sitter model in general relativity with an exponential ‘runaway’ expansion.

Dark Gravity

As we discuss this no dark matter alternative, we refer to it as dark gravity, or dark acceleration. Regardless of the nature of dark matter and dark gravity, the combination of ordinary gravity and dark gravity is still insufficient to halt the expansion of the universe. In this view, the dark gravity is due to ordinary matter, there is just more of it (gravity) than we expect, again only for the very low c * H or lower acceleration environments.

Some of the proposed laws for modified gravity are:

  1. MOND – Modified Newtonian Dynamics, from Milgrom
  2. Emergent gravity, from Verlinde
  3. Metric skew tensor gravity (MSTG), from Moffat (and also the more recent variant scalar-tensor-vector gravity (STVG), sometimes called MOG (Modified gravity)

Think of the dark gravity as an additional term in the equations, beyond the gravity we are familiar with. Each of the models adds an additional term to Newtonian gravity, that only becomes significant for accelerations less than c*H. The details vary between the proposed alternatives. All do a good job of matching galaxy rotation curves for spiral galaxies and the Tully-Fisher relation that can be used for analyzing elliptical galaxies.

Things are trickier in clusters of galaxies, which are observed for galaxy velocity dispersions, X-ray emission of intracluster gas, and gravitational lensing. The MOND model appears to come up short by a factor of about two in explaining the total dark gravity implied.

Emergent gravity and modified gravity theories including MSTG claim to be able to match the observations in clusters.

Clusters of Galaxies

Most galaxies are found in groups and clusters.

Clusters and groups form from the collapse of overdense regions of hydrogen and helium gas in the early universe. Collapsing under its own gravity, such a region will heat up via frictional processes and cooler sub-regions will collapse further to form galaxies within the cluster.

Rich clusters have hundreds, even thousands of galaxies, and their gravitational potential is so high that the gas is heated to millions of degrees via friction and shock waves and gives off X-rays. The X-ray emission from clusters has been actively studied since the 1970s, via satellite experiments.

What is found is that most matter is in the form of intracluster gas, not galaxies. Some of this is left over primordial gas that never formed galaxies and some is gas that was once in a galaxy but expelled via energetic processes, especially supernovae.

Observations indicate that around 90% of (ordinary) matter is in the form of intracluster gas, and only around 10% within the galaxies in the form of stars or interstellar gas and dust. Thus modeling the mass profile of a cluster is best done by looking at how the X-ray emission falls off as one moves away from the center of a cluster.

In their 2005 paper, Brownstein and Moffat compiled X-ray emission profiles and fit gas mass profiles with radius and temperature profiles for 106 galaxy clusters. They aggregated data from a sample of 106 clusters and find that an MSTG model can reproduce the X-ray emission with a mass profile that does not require dark matter.

The figure below shows the average profile of cumulative mass interior to a given radius. The mass is in units of solar masses and runs into the hundreds of trillions. The average radius extends to over 1000 Kiloparsecs or over 1 Megaparsec (a parsec is 3.26 light-years).

The bottom line is that emergent gravity and MSTG both claim to have explanatory power without any dark matter for observations of galaxy rotation curves, gravitation lensing in clusters (Brower et al. 2016), and cluster mass profiles deduced from the X-ray emission from hot gas.

galaxyclustermasseswodm.fig2

Figure 2 from J.R. Brownstein⋆ and J.W. Moffat (2005), “Galaxy Cluster Masses without Non-Baryonic Dark Matter”. Shown is cumulative mass required as a function of radius. The red curve is the average of X-ray observations from a sample of 106 clusters. The black curve is the authors’ model assuming MSTG, a good match. The cyan curve is the MOND model, the blue curve is a Newtonian model, and both require dark matter. The point is that the authors can match observations with much less matter and there is no need to postulate additional exotic dark matter.

What we would very much like to see is a better explanation of the cosmic microwave background density perturbation spectrum for the cosmic scale, for either of these dark gravity models. The STVG variant of MSTG claims to address those observations as well, without the need for dark matter.

In future posts we may look at that issue and also the so called ‘silver bullet’ that dark matter proponents often promote, the Bullet Cluster, that consists of two galaxy clusters colliding and a claimed separation of dark matter and gas.

References

Brower, M. et al. 2016, “First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing Measurements” https://arxiv.org/abs/1612.03034v2

Brownstein, J. and Moffat, J. 2005, “Galaxy Cluster Masses without Non-baryonic Dark Matter”, https://arxiv.org/abs/astro-ph/0507222

Perrenod, S. 1977 “The Evolution of Cluster X-ray Sources” http://adsabs.harvard.edu/abs/1978ApJ…226..566P, thesis.

https://darkmatterdarkenergy.com/2018/09/19/matter-and-energy-tell-spacetime-how-to-be-dark-gravity/

https://darkmatterdarkenergy.com/2016/12/30/emergent-gravity-verlindes-proposal/

https://darkmatterdarkenergy.com/2016/12/09/modified-newtonian-dynamics-is-there-something-to-it/

3 Comments   |  tags: , , , , , , , , , | posted in Dark Matter, Gravity

February 11, 2018

Unified Physics including Dark Matter and Dark Energy

By Stephen Perrenod

Dark matter keeps escaping direct detection, whether it might be in the form of WIMPs, or primordial black holes, or axions. Perhaps it is a phantom and general relativity is inaccurate for very low accelerations. Or perhaps we need a new framework for particle physics other than what the Standard Model and supersymmetry provide.

We are pleased to present a guest post from Dr. Thomas J. Buckholtz. He introduces us to a theoretical framework referred to as CUSP, that results in four dozen sets of elementary particles. Only one of these sets is ordinary matter, and the framework appears to reproduce the known fundamental particles. CUSP posits ensembles that we call dark matter and dark energy. In particular, it results in the approximate 5:1 ratio observed for the density of dark matter relative to ordinary matter at the scales of galaxies and clusters of galaxies. (If interested, after reading this post, you can read more at his blog linked to his name just below).

Thomas J. Buckholtz

My research suggests descriptions for dark matter, dark energy, and other phenomena. The work suggests explanations for ratios of dark matter density to ordinary matter density and for other observations. I would like to thank Stephen Perrenod for providing this opportunity to discuss the work. I use the term CUSP – concepts uniting some physics – to refer to the work. (A book, Some Physics United: With Predictions and Models for Much, provides details.)

CUSP suggests that the universe includes 48 sets of elementary-particle Standard Model elementary particles and composite particles. (Known composite particles include the proton and neutron.) The sets are essentially (for purposes of this blog) identical. I call each instance an ensemble. Each ensemble includes its own photon, Higgs boson, electron, proton, and so forth. Elementary particle masses do not vary by ensemble. (Weak interaction handedness might vary by ensemble.)

One ensemble correlates with ordinary matter, 5 ensembles correlate with dark matter, and 42 ensembles contribute to dark energy densities. CUSP suggests interactions via which people might be able to detect directly (as opposed to infer indirectly) dark matter ensemble elementary particles or composite particles. (One such interaction theoretically correlates directly with Larmor precession but not as directly with charge or nominal magnetic dipole moment. I welcome the prospect that people will estimate when, if not now, experimental techniques might have adequate sensitivity to make such detections.)

Buckholtztable

This explanation may describe (much of) dark matter and explain (at least approximately some) ratios of dark matter density to ordinary matter density. You may be curious as to how I arrive at suggestions CUSP makes. (In addition, there are some subtleties.)

Historically regarding astrophysics, the progression ‘motion to forces to objects’ pertains. For example, Kepler’s work replaced epicycles with ellipses before Newton suggested gravity. CUSP takes a somewhat reverse path. CUSP models elementary particles and forces before considering motion. The work regarding particles and forces matches known elementary particles and forces and extrapolates to predict other elementary particles and forces. (In case you are curious, the mathematics basis features solutions to equations featuring isotropic pairs of isotropic quantum harmonic oscillators.)

I (in effect) add motion by extending CUSP to embrace symmetries associated with special relativity. In traditional physics, each of conservation of angular momentum, conservation of momentum, and boost correlates with a spatial symmetry correlating with the mathematics group SU(2). (If you would like to learn more, search online for “conservation law symmetry,” “Noether’s theorem,” “special unitary group,” and “Poincare group.”) CUSP modeling principles point to a need to add to temporal symmetry and, thereby, to extend a symmetry correlating with conservation of energy to correlate with the group SU(7). The number of generators of a group SU(n) is n2−1. SU(7) has 48 generators. CUSP suggests that each SU(7) generator correlates with a unique ensemble. (In case you are curious, the number 48 pertains also for modeling based on either Newtonian physics or general relativity.)

CUSP math suggests that the universe includes 8 (not 1 and not 48) instances of traditional gravity. Each instance of gravity interacts with 6 ensembles.

The ensemble correlating with people (and with all things people see) connects, via our instance of gravity, with 5 other ensembles. CUSP proposes a definitive concept – stuff made from any of those 5 ensembles – for (much of) dark matter and explains (approximately) ratios of dark matter density to ordinary matter density for the universe and for galaxy clusters. (Let me not herein do more than allude to other inferably dark matter based on CUSP-predicted ordinary matter ensemble composite particles; to observations that suggest that, for some galaxies, the dark matter to ordinary matter ratio is about 4 to 1, not 5 to 1; and other related phenomena with which CUSP seems to comport.)

CUSP suggests that interactions between dark matter plus ordinary matter and the seven peer combinations, each comprised of 1 instance of gravity and 6 ensembles, is non-zero but small. Inferred ratios of density of dark energy to density of dark matter plus ordinary matter ‘grow’ from zero for observations pertaining to somewhat after the big bang to 2+ for observations pertaining to approximately now. CUSP comports with such ‘growth.’ (In case you are curious, CUSP provides a nearly completely separate explanation for dark energy forces that govern the rate of expansion of the universe.)

Relationships between ensembles are reciprocal. For each of two different ensembles, the second ensemble is either part of the first ensemble’s dark matter or part of the first ensemble’s dark energy. Look around you. See what you see. Assuming that non-ordinary-matter ensembles include adequately physics-savvy beings, you are looking at someone else’s dark matter and yet someone else’s dark energy stuff. Assuming these aspects of CUSP comport with nature, people might say that dark matter and dark-energy stuff are, in effect, quite familiar.

Copyright © 2018 Thomas J. Buckholtz

 

1 Comment   |  tags: , , , , , , , | posted in Dark Energy, Dark Matter

July 13, 2017

Dark Energy and the Cosmological Constant

By Stephen Perrenod

I am seeing a lot of confusion around dark energy and the cosmological constant. What are they? Is gravity always attractive? Or is there such a thing as negative gravity or anti-gravity?

First, what is gravity? Einstein taught us that it is the curvature of space. Or as famous relativist John Wheeler wrote “Matter tells space how to curve, and curved space tells matter how to move”.

Dark Energy has been recognized with the Nobel Prize for Physics, so its reality is accepted. There were two teams racing against one another and they found the same result in 1998: the expansion of the universe is accelerating!

Normally one would have thought it would be slowing down due to the matter within; both ordinary and dark matter would work to slow the expansion. But this is not observed for distant galaxies. One looks at a certain type of supernova that always has a certain mass and thus the same absolute luminosity. So the apparent brightness can be used to determine the luminosity distance. This is compared with the redshift that provides the velocity of recession or velocity-determined distance in accordance with Hubble’s law.

A comparison of the two types of distance measures, particularly for large distances, shows the unexpected acceleration. The most natural explanation is a dark energy component equal to twice the matter component, and that matter component would include any dark matter. Now do not confuse dark energy with dark matter. The latter contributes to gravity in the normal way in proportion to its mass. Like ordinary matter it appears to be non-relativistic and without pressure.

Einstein presaged dark energy when he added the cosmological constant term to his equations of general relativity in 1917. He was trying to build a static universe. It turns out that such a model is unstable, and he later called his insertion of the cosmological constant a blunder. A glorious blunder it was, as we learned eight decades later!

Here is the equation:

G_{ab}+\Lambda g_{ab} = {8\pi G \over c^{4}}T_{ab}

The cosmological constant is represented by the Λ term, and interestingly it is usually written on the left hand side with the metric terms, not on the right hand side with the stress-energy (and pressure and mass) tensor T.

If we move it to the right hand side and express as an energy density, the term looks like this:

\rho  = {\Lambda \over8\pi G }

with \rho  as the vacuum energy density or dark energy, and appearing on the right it also takes a negative sign. So this is a suggestion as to why it is repulsive.

The type of dark energy observed in our current universe can be fit with the simple cosmological constant model and it is found to be positive. So if you move \Lambda to the other side of the equation, it enters negatively.

Now let us look at dark energy more generally. It satisfies an equation of state defined by the relationship of pressure to density, with P as pressure and ρ denoting density:

P = w \cdot \rho \cdot c^2

Matter, whether ordinary or dark, is to first order pressureless for our purposes, quantified by its rest mass, and thus takes w = 0. Radiation it turns out has w = 1/3. The dark energy has a negative w, which is why you have heard the phrase ‘negative pressure’. The simplest case is w = -1, which the cosmological constant, a uniform energy density independent of location and age of the universe. Alternative models of dark energy known as quintessence can have a larger w, but it must be less than -1/3.

275px-EquationofState.gif

Credit: http://www.scholarpedia.org/article/Cosmological_constant

Why less than -1/3? Well the equations of general relativity as a set of nonlinear differential equations are usually notoriously difficult to solve, and do not admit of analytical solutions. But our universe appears to be highly homogeneous and isotropic, so one can use a simple FLRW spherical metric, and in this case one end up with the two Friedmann equations (simplified by setting c =1).

\ddot a/a  = - {4 \pi  G \over 3} ({\rho + 3 p}) + {\Lambda \over 3 }

This is for a (k = 0) flat on large scales universe as observed. Here \ddot a is the acceleration (second time derivative) of the scale factor a. So if \ddot a is positive, the expansion of the universe is speeding up.

The \Lambda term can be rewritten using the dark energy density relation above. Now the equation needs to account for both matter (which is pressureless, whether it is ordinary or dark matter) and dark energy. Again the radiation term is negligible at present, by four orders of magnitude. So we end up with:

\ddot a/a  = - {4 \pi  G \over 3} ({\rho_m + \rho_{de} + 3 p_{de}})

Now the magic here was in the 3 before the p. The pressure gets 3 times the weighting in the stress-energy tensor T. Why, because energy density is just there as a scalar, but pressure must be accounted for in each of the 3 spatial dimensions. And since p for dark energy is negative and equal to the dark energy density (times the square of the speed of light), then

\rho + 3 p is always negative for the dark energy terms, provided w < -1/3. That unusual behavior is why we call it ‘dark energy’.

Overall it is a battle between matter and dark energy density on the one side, and dark energy pressure (being negative and working oppositely to how we ordinarily think of gravity) on the other. The matter contribution gets weaker over time, since as the universe expands the matter becomes less dense by a relative factor of (1=z)^3 , that is the matter was on average denser in the past by the cube of one plus the redshift for that era.

Dark energy eventually wins out, because it, unlike matter does not thin out with the expansion. Every cubic centimeter of space, including newly created space with the expansion has its own dark energy, generally attributed to the vacuum. Due to the quantum uncertainty (Heisenberg) principle, even the vacuum has fields and non zero energy.

Now the actual observations at present for our universe show, in units of the critical density that

\rho_m \approx 1/3

\rho_{de} \approx 2/3

and thus

p_{de} \approx - 2

And the sum of them all is around -1, just coincidentally. Since there is a minus sign in front of the whole thing, the acceleration of the universe is positive. This is all gravity, it is just that some terms take the opposite side. The idea that gravity can only be attractive is not correct.

If we go back in time, say to the epoch when matter still dominated with \rho_m \approx 2/3 and  \rho_{de} \approx 1/3 , then the total including pressure would be 2/3 +1/3 – 1, or 0.

That would be the epoch when the universe changed from decelerating to accelerating, as dark energy came to dominate. With our present cosmological parameters, it corresponds to a redshift of z \approx 0.6, and almost 6 billion years ago.

Image: NASA/STScI, public domain

3 Comments   |  tags: , , , , | posted in Dark Energy

December 30, 2016

Emergent Gravity: Verlinde’s Proposal

By darkmatterdarkenergy

In a previous blog entry I give some background around Erik Verlinde’s proposal for an emergent, thermodynamic basis of gravity. Gravity remains mysterious 100 years after Einstein’s introduction of general relativity – because it is so weak relative to the other main forces, and because there is no quantum mechanical description within general relativity, which is a classical theory.

One reason that it may be so weak is because it is not fundamental at all, that it represents a statistical, emergent phenomenon. There has been increasing research into the idea of emergent spacetime and emergent gravity and the most interesting proposal was recently introduced by Erik Verlinde at the University of Amsterdam in a paper “Emergent Gravity and the Dark Universe”.

A lot of work has been done assuming anti-de Sitter (AdS) spaces with negative cosmological constant Λ – just because it is easier to work under that assumption. This year, Verlinde extended this work from the unrealistic AdS model of the universe to a more realistic de Sitter (dS) model. Our runaway universe is approaching a dark energy dominated dS solution with a positive cosmological constant Λ.

The background assumption is that quantum entanglement dictates the structure of spacetime, and its entropy and information content. Quantum states of entangled particles are coherent, observing a property of one, say the spin orientation, tells you about the other particle’s attributes; this has been observed in long distance experiments, with separations exceeding 100 kilometers.

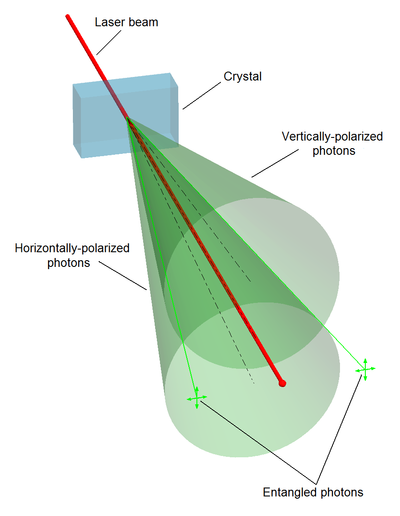400px-SPDC_figure.pngIf space is defined by the connectivity of quantum entangled particles, then it becomes almost natural to consider gravity as an emergent statistical attribute of the spacetime. After all, we learned from general relativity that “matter tells space how to curve, curved space tells matter how to move” – John Wheeler.

What if entanglement tells space how to curve, and curved space tells matter how to move? What if gravity is due to the entropy of the entanglement? Actually, in Verlinde’s proposal, the entanglement entropy from particles is minor, it’s the entanglement of the vacuum state, of dark energy, that dominates, and by a very large factor.

One analogy is thermodynamics, which allows us to represent the bulk properties of the atmosphere that is nothing but a collection of a very large number of molecules and their micro-states. Verlinde posits that the information and entropy content of space are due to the excitations of the vacuum state, which is manifest as dark energy.

The connection between gravity and thermodynamics has been around for 3 decades, through research on black holes, and from string theory. Jacob Bekenstein and Stephen Hawking determined that a black hole possesses entropy proportional to its area divided by the gravitational constant G. String theory can derive the same formula for quantum entanglement in a vacuum. This is known as the AdS/CFT (conformal field theory) correspondence.

So in the AdS model, gravity is emergent and its strength, the acceleration at a surface, is determined by the mass density on that surface surrounding matter with mass M. This is just the inverse square law of Newton. In the more realistic dS model, the entropy in the volume, or bulk, must also be considered. (This is the Gibbs entropy relevant to excited states, not the Boltzmann entropy of a ground state configuration).

Newtonian dynamics and general relativity can be derived from the surface entropy alone, but do not reflect the volume contribution. The volume contribution adds an additional term to the equations, strengthening gravity over what is expected, and as a result, the existence of dark matter is ‘spoofed’. But there is no dark matter in this view, just stronger gravity than expected.

This is what the proponents of MOND have been saying all along. Mordehai Milgrom observed that galactic rotation curves go flat at a characteristic low acceleration scale of order 2 centimeters per second per year. MOND is phenomenological, it observes a trend in galaxy rotation curves, but it does not have a theoretical foundation.

Verlinde’s proposal is not MOND, but it provides a theoretical basis for behavior along the lines of what MOND states.

Now the volume in question turns out to be of order the Hubble volume, which is defined as c/H, where H is the Hubble parameter denoting the rate at which galaxies expand away from one another. Reminder: Hubble’s law is v = H \cdot d where v is the recession velocity and the d the distance between two galaxies. The lifetime of the universe is approximately 1/H.

clusters_1280.abell1835.jpg

The value of c / H is over 4 billion parsecs (one parsec is 3.26 light-years) so it is in galaxies, clusters of galaxies, and at the largest scales in the universe for which departures from general relativity (GR) would be expected.

Dark energy in the universe takes the form of a cosmological constant Λ, whose value is measured to be 1.2 \cdot 10^{-56} cm^{-2} . Hubble’s parameter is 2.2 \cdot 10^{-18} sec^{-1} . A characteristic acceleration is thus H²/ sqrt(Λ) or 4 \cdot 10^{-8}  cm per sec per sec (cm = centimeters, sec = second).

One can also define a cosmological acceleration scale simply by c \cdot H , the value for this is about 6 \cdot 10^{-8} cm per sec per sec (around 2 cm per sec per year), and is about 15 billion times weaker than Earth’s gravity at its surface! Note that the two estimates are quite similar.

This is no coincidence since we live in an approximately dS universe, with a measured  Λ ~ 0.7 when cast in terms of the critical density for the universe, assuming the canonical ΛCDM cosmology. That’s if there is actually dark matter responsible for 1/4 of the universe’s mass-energy density. Otherwise Λ could be close to 0.95 times the critical density. In a fully dS universe, \Lambda \cdot c^2 = 3 \cdot H^2 , so the two estimates should be equal to within sqrt(3) which is approximately the difference in the two estimates.

So from a string theoretic point of view, excitations of the dark energy field are fundamental. Matter particles are bound states of these excitations, particles move freely and have much lower entropy. Matter creation removes both energy and entropy from the dark energy medium. General relativity describes the response of area law entanglement of the vacuum to matter (but does not take into account volume entanglement).

Verlinde proposes that dark energy (Λ) and the accelerated expansion of the universe are due to the slow rate at which the emergent spacetime thermalizes. The time scale for the dynamics is 1/H and a distance scale of c/H is natural; we are measuring the time scale for thermalization when we measure H. High degeneracy and slow equilibration means the universe is not in a ground state, thus there should be a volume contribution to entropy.

When the surface mass density falls below c \cdot H / (8 \pi \cdot G) things change and Verlinde states the spacetime medium becomes elastic. The effective additional ‘dark’ gravity is proportional to the square root of the ordinary matter (baryon) density and also to the square root of the characteristic acceleration c \cdot H.

This dark gravity additional acceleration satisfies the equation g _D = sqrt  {(a_0 \cdot g_B / 6 )} , where g_B is the usual Newtonian acceleration due to baryons and a_0 = c \cdot H is the dark gravity characteristic acceleration. The total gravity is g = g_B + g_D . For large accelerations this reduces to the usual g_B and for very low accelerations it reduces to sqrt  {(a_0 \cdot g_B / 6 )} .

The value a_0/6 at 1 \cdot 10^{-8} cm per sec per sec derived from first principles by Verlinde is quite close to the MOND value of Milgrom, determined from galactic rotation curve observations, of 1.2 \cdot 10^{-8} cm per sec per sec.

So suppose we are in a region where g_B is only 1 \cdot 10^{-8} cm per sec per sec. Then g_D takes the same value and the gravity is just double what is expected. Since orbital velocities go as the square of the acceleration then the orbital velocity is observed to be sqrt(2) higher than expected.

In terms of gravitational potential, the usual Newtonian potential goes as 1/r, resulting in a 1/r^2 force law, whereas for very low accelerations the potential now goes as log(r) and the resultant force law is 1/r. We emphasize that while the appearance of dark matter is spoofed, there is no dark matter in this scenario, the reality is additional dark gravity due to the volume contribution to the entropy (that is displaced by ordinary baryonic matter).

M33_rotation_curve_HI.gif

Flat to rising rotation curve for the galaxy M33

Dark matter was first proposed by Swiss astronomer Fritz Zwicky when he observed the Coma Cluster and the high velocity dispersions of the constituent galaxies. He suggested the term dark matter (“dunkle materie”). Harold Babcock in 1937 measured the rotation curve for the Andromeda galaxy and it turned out to be flat, also suggestive of dark matter (or dark gravity). Decades later, in the 1970s and 1980s, Vera Rubin (just recently passed away) and others mapped many rotation curves for galaxies and saw the same behavior. She herself preferred the idea of a deviation from general relativity over an explanation based on exotic dark matter particles. One needs about 5 times more matter, or about 5 times more gravity to explain these curves.

Verlinde is also able to derive the Tully-Fisher relation by modeling the entropy displacement of a dS space. The Tully-Fisher relation is the strong observed correlation between galaxy luminosity and angular velocity (or emission line width) for spiral galaxies, L \propto v^4 .  With Newtonian gravity one would expect M \propto v^2 . And since luminosity is essentially proportional to ordinary matter in a galaxy, there is a clear deviation by a ratio of v².

massdistribution.jpeg

 Apparent distribution of spoofed dark matter,  for a given ordinary (baryonic) matter distribution

When one moves to the scale of clusters of galaxies, MOND is only partially successful, explaining a portion, coming up shy a factor of 2, but not explaining all of the apparent mass discrepancy. Verlinde’s emergent gravity does better. By modeling a general mass distribution he can gain a factor of 2 to 3 relative to MOND and basically it appears that he can explain the velocity distribution of galaxies in rich clusters without the need to resort to any dark matter whatsoever.

And, impressively, he is able to calculate what the apparent dark matter ratio should be in the universe as a whole. The value is \Omega_D^2 = (4/3) \Omega_B where \Omega_D is the apparent mass-energy fraction in dark matter and \Omega_B is the actual baryon mass density fraction. Both are expressed normalized to the critical density determined from the square of the Hubble parameter, 8 \pi G \rho_c = 3 H^2 .

Plugging in the observed \Omega_B \approx 0.05 one obtains \Omega_D \approx 0.26 , very close to the observed value from the cosmic microwave background observations. The Planck satellite results have the proportions for dark energy, dark matter, ordinary matter as .68, .27, and .05 respectively, assuming the canonical ΛCDM cosmology.

The main approximations Verlinde makes are a fully dS universe and an isolated, static (bound) system with a spherical geometry. He also does not address the issue of galaxy formation from the primordial density perturbations. At first guess, the fact that he can get the right universal \Omega_D suggests this may not be a great problem, but it requires study in detail.

Breaking News!

Margot Brouwer and co-researchers have just published a test of Verlinde’s emergent gravity with gravitational lensing. Using a sample of over 33,000 galaxies they find that general relativity and emergent gravity can provide an equally statistically good description of the observed weak gravitational lensing. However, emergent gravity does it with essentially no free parameters and thus is a more economical model.

“The observed phenomena that are currently attributed to dark matter are the consequence of the emergent nature of gravity and are caused by an elastic response due to the volume law contribution to the entanglement entropy in our universe.” – Erik Verlinde

References

Erik Verlinde 2011 “On the Origin of Gravity and the Laws of Newton” arXiv:1001.0785

Stephen Perrenod, 2013, 2nd edition, “Dark Matter, Dark Energy, Dark Gravity” Amazon, provides the traditional view with ΛCDM  (read Dark Matter chapter with skepticism!)

Erik Verlinde 2016 “Emergent Gravity and the Dark Universe arXiv:1611.02269v1

Margot Brouwer et al. 2016 “First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing Measurements” arXiv:1612.03034v

9 Comments   |  tags: , , , , , , , , , , , , , , , , | posted in Dark Energy, Dark Matter, Gravity

February 17, 2016

Gravitational Waves and Dark Matter, Dark Energy

By Stephen Perrenod

What does the discovery of gravitational waves imply about dark matter and dark energy?

The first detection of gravitational waves results from a pair of merging black holes, and is yet another magnificent confirmation of the theory of general relativity. Einstein’s theory of general relativity has passed every test thrown at it during the last 100 years.

While the existence of gravitational waves was fully expected to be confirmed, the discovery took several decades and represents a technological tour de force. Detected at the two LIGO sites, one in Louisiana and one in Washington State, the main event lasted only 0.2 seconds, and was seen as a change of length in the “arms” of the detector (laser interferometers) of only one part in a thousand billion billion.

LIGO signal 2

The LIGO detection of gravitational waves. The blue curve is from the Louisiana site and the red curve from the Washington state site. The two curves are shifted by 7 milliseconds to account for the speed-of-light delay between the two sites. Note that most of the power in the signal occurs within less than 0.2 seconds. The strain is a measure of proportional change in length of the detector arm and is less than 1 part in 10²¹.

Nevertheless, this is the most energetic event ever seen by mankind. The merger of two large black holes totaling over 60 times the Sun’s mass resulted in the conversion of 3 solar masses of material into gravitational wave energy. Imagine, there were 3 Suns worth of matter obliterated in the blink of an eye. During this brief period, the generated power was greater than that from the light of all of the stars of all of the galaxies in our known universe.

What the discovery of gravitational waves has to say about dark matter and dark energy is essentially that it further confirms their existence.

Although there is as of now no direct detection of dark matter, we infer the existence of dark matter by using the equations of general relativity (GR), in a number of cases, including:

  1. Gravitational lensing – Typically, a foreground cluster of galaxies distorts and magnifies the image of a background galaxy. GR is used to calculate the bending and magnification, primarily caused by the dark matter in the foreground cluster.
  2. Cosmic microwave background radiation (CMBR) – The CMBR has spatial fluctuation peaks (harmonics) and the first peak tells us about ordinary matter and the third peak about the density of dark matter. A GR-based cosmological model is used to determine the dark matter average density.

Dark matter is also inferred from the way in which galaxies rotate and from the velocities of galaxies within galaxy clusters, but general relativity is not needed to calculate the dark matter densities in such cases. However, results from these methods are consistent with results from the methods listed above.

In the case of dark energy, it turns out to be a parameter in the equations of general relativity as first formulated by Einstein. The parameter, lambda, (Λ) is known as the cosmological constant, and represents the minimum energy of the vacuum. For many years astronomers and cosmologists thought it might take the value of zero. However in 1998 multiple teams confirmed that the value is positive and not zero, and it turns out that dark energy has more than twice the energy content of dark matter. Its non-zero value is actually another stunning success for general relativity.

Thus the detection of gravitational waves indirectly provides further support for the canonical cosmological model ΛCDM, with both dark matter and dark energy, and fully consistent with general relativity.

References

http://www.sciencemag.org/news/2016/02/gravitational-waves-einstein-s-ripples-spacetime-spotted-first-time – ScienceMag article

B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 116, 061102 – Published 11 February 2016 – http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.061102

NEW BOOK just released:

S. Perrenod, 2016, 72 Beautiful Galaxies (especially designed for iPad, iOS; ages 12 and up)

Andromeda_galaxy_Galex

Leave a comment   |  tags: , , , , , , , | posted in Dark Energy, Dark Matter

April 21, 2015

X-raying Dark Matter

By darkmatterdarkenergy

I was at the dentist this week. Don’t ask, but they took 3 digital X-Rays.

One of the most significant methods by which we detect the presence of dark matter is through the use of X-ray telescopes. The energy associated with these X-rays is typically around an order of magnitude less than those zapped into your mouth when you visit the dentist.

Around 50 years ago scientists at American Science and Engineering flew the first imaging X-ray telescope on a small rocket. At a later date, I worked part-time at AS&E, as we called it, while in graduate school. One major project was a solar X-Ray telescope mounted in SkyLab, America’s first space station. This gave me the wonderful opportunity to work in the control rooms at the NASA Johnson Space Center in Houston.

X-rays are absorbed in the Earth’s atmosphere, so today X-ray astronomy is performed from orbiting satellites. X-ray telescopes use the principle of grazing incidence reflection; the X-rays impinge at shallow angles onto gold or iridium-coated metallic surfaces and are reflected to the focal plane and the detector electronics.

cxcmirrors-72

Schematic of grazing incidence mirrors used in the Chandra X-ray Observatory. Credit NASA/CXC/SAO; obtained from chandra.harvard.edu.

How does dark matter result in X-rays being produced? Indirectly, as a consequence of its gravitational effects.

One of the main mechanisms for X-ray production in the universe is known as thermal bremsstrahlung. Bremsstrahlung is a German word meaning ‘decelerated radiation’. A gas which is hot enough to give off X-rays will be ionized. That is, the electrons will be stripped from the nuclei and move about freely. As electrons fly around near ions (protons and helium nuclei primarily) their mutual electromagnetic attraction will result in some of the electrons’ kinetic energy being transferred to radiation.

The speed at which the electrons are moving around determines how energetic the produced photons will be. We talk about the temperature of such an ionized gas, and that is proportional to the square of the average speed of the electrons. A gas with a temperature of 10 million degrees will give off approximately 1 kiloVolt X-rays (hereafter we use the KeV abbreviation), and a gas with a temperature of 100 million degrees will radiate 10 KeV X-rays. One eV converts to 11,605 degrees Kelvin (or we can just say Kelvins).

ChandrainColumbiabay

Chandra X-ray Observatory prior to launch in the Space Shuttle Columbia in 1999. NASA image.

So how can we produce gas hot enough to give off X-Rays by this mechanism? Gravity, and lots of it. The potential energy of the gravitational field is proportional to the amount of matter (total mass) coalesced into a region and inversely proportional to the characteristic scale of that region. GM/R, simple Newtonian mechanics, is sufficient; no general relativistic calculation is needed at this point. G is the gravitational constant and M and R are the cluster mass and characteristic radius, respectively.

A lot of mass in a confined region – how about large groups of clusters and galaxies? It turns out we need of order 1000 galaxies for a rich cluster and this will do the trick. But only because there is dark matter as well as ordinary matter. There are three main matter components to consider: galaxies, hot intracluster gas found between galaxies, and dark matter. The cluster forms from gravitational self-collapse from a region that was of above average density in the early universe. All the over dense regions are subject to collapse.

darkmatter.bulletcluster

The “Bullet Cluster” is actually two colliding clusters. The bluish color shows the distribution of dark matter as determined from the gravitational lensing effect on background galaxy images. The reddish color depicts the hot X-ray emitting gas measured by the Chandra X-ray Observatory.

(X-ray: NASA/CXC/CfA/M.Markevitch Optical: NASA/STScI; Magellan/U.Arizona/D.Clowe Lensing Map: NASA/STScI; ESO WFI; Magellan/U.Arizona/D.Clowe)

The optically visible galaxies are the least important contributor to the cluster mass, only around 1%! Galaxy clusters are made of dark matter much more than they are made out of galaxies. And secondarily, they are made out of hot gas. The ordinary matter contained within galaxies is only the third most important component. The table below gives the typical 90 / 9 / 1 proportions for dark matter, hot gas, and galaxies, respectively.

Three main components of a galaxy cluster (Table derived from Wikipedia article on galaxy clusters)

Component                      Mass fraction             Description

Galaxies                           1%                         Optical/infrared observations

Intergalactic gas              9%                         High temperature ionized gas – thermal bremsstrahlung

Dark matter                     90%                        Dominates, inferred through gravitational interactions

The intracluster gas has two sources. A major portion of it is primordial gas that never formed galaxies, but falls into the gravitational potential well of the cluster. As it falls in toward the cluster center, it heats. The kinetic energy of infall is converted to random motions of the ionized gas. An additional portion of the gas is recycled material expelled from galaxies. It mixes with the primordial gas and heats up as well through frictional processes. The gas is supported against further collapse by its own pressure as the density and temperature increase in the cluster core.

The temperature which characterizes the X-ray emission is a measure of gravitational potential strength and proportional to the ratio of the mass of the cluster to its size. Typical X-Ray temperatures measured for rich clusters are around 3 to 12 KeV, which corresponds to temperatures in the range of 30 to 130 million Kelvins.

There is another way to measure the strength of the cluster’s gravitational potential well. That is by measuring the speed of galaxies as they move around in somewhat random fashion inside the cluster. The assumption, which is valid for well-formed clusters after they have been around for billions of years, is that the galaxies are not just falling into the center of the cluster, but that their motions are “virialized”. This is the method used by Fritz Zwicky in the 1930s for the original discovery of dark matter. He found that in a certain well known cluster, the Coma cluster, that the average speed of galaxies relative to the cluster centroid was of order 1000 kilometers/sec, much higher than the expected 300 km/sec based on the visible light from the cluster galaxies. This implied 10 times as much dark matter as galactic matter. This early, rather crude measurement, was on the right track, but fell short of the actual ratio of dark matter to galactic matter since we now know that galaxies themselves have large dark matter halos. The X-ray emission from clusters was discovered much later, starting in the 1970s.

The two methods of measuring the amount of dark matter in Galaxy clusters generally agree. Both the galaxies and the hot intracluster gas are acting as tracers of the overall mass distribution, which is dominated by dark matter. Galaxy clusters play a major role in increasing our understanding of dark matter and how it affects the formation and evolution of galaxies.

In fact if dark matter was not 5 times as abundant by mass as ordinary matter, most galaxy clusters would never have formed, and galaxies such as our own Milk Way would be much smaller.

References

Wikipedia article “galaxy clusters”.

“X-ray Temperatures of Distant Clusters of Galaxies”, S. C. Perrenod,  J. P. Henry 1981, Astrophysical Journal, Letters to the Editor, vol. 247, p. L1-L4.

“The X-ray Luminosity – Velocity Dispersion Relation in the REFLEX Cluster Survey”, A. Ortiz-Gil, L. Guzzo, P. Schuecker, H. Boehringer, C.A. Collins 2004, Mon.Not.Roy.Astron.Soc. 348, 325; http://arxiv.org/abs/astro-ph/0311120v1

Leave a comment   |  tags: , , , , , , , , , , | posted in Dark Matter

February 28, 2011

Scale of the universe

By darkmatterdarkenergy
Hubble Ultradeep Field

Hubble Ultra Deep Field

Until 500 years ago the premise of an Earth-centric solar system and universe prevailed. And until 100 years ago it was thought that we lived within the confines of a single galaxy, our Milky Way. But in 1915 Albert Einstein introduced general relativity, the highly successful theory of gravity which couples mass, energy and the geometry of space-time. In the 1920s Alexander Friedmann and Georges Lemaitre introduced solutions to the equations of general relativity for an expanding universe. Lemaitre’s work indicated distant galaxies would have their light shifted to be redder than that of nearby galaxies. And by 1929 this was observed by Edwin Hubble. Now with the Hubble Space Telescope we can observe galaxies at much greater distances than Hubble could over 80 years ago. The image above is a very long exposure from the Hubble Space Telescope revealing close to 10,000 galaxies; many of these are billions of light-years away.

Hubble essentially measured the rate of expansion of the universe at the present epoch. The universe is expanding and galaxies are generally receding from one another except when they are gravitationally bound to their near neighbors. The value for the rate of expansion has been refined over the intervening years but is now accurately measured and indicates an age of just under 14 billion years for our universe.

The size of the universe as a whole we are unable to measure! We are limited by our own horizon, due to the finite speed of light. Only galaxies apparently moving away from us at less than the speed of light are within our horizon (also known as light cone). General relativity allows for space itself to stretch at faster than the speed of light if the separations between two galaxies are large enough; objects do not travel faster than light speed within their own local frame.

Our own observable portion of the universe has a lookback time distance of 14 billion light-years and what is known as the comoving distance of nearly 50 billion light-years. The comoving distance takes into account the expansion of the universe as the light moves through it from the Big Bang until now.

Note from the table below how much larger the universe is than the distance to the center of our galaxy or to the nearest star.

Object                    Distance (light travel time)

Nearest Star                        4.2 years
Center of Milky Way         25,000 years
Andromeda Galaxy           2.5 million years
Oldest Galaxies                  13 billion years
Big Bang                              13.8 billion years

Leave a comment   |  tags: , , | posted in Big Bang & Inflation